练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，一圆弧形钢梁的拱高CD为8m，跨径AB为40m，则这钢梁圆弧的半径是（　　）
    A．28mB．29mC．30mD．31m

    分析 将拱形图进行补充，构造直角三角形，利用勾股定理和垂径定理解答

    解答 解：延长CD到O，使得OC=OA，则O为圆心，
    ∵圆弧形钢梁的跨度AB=40m，拱高CD=8m，
    ∴AD=20m，
    ∴AD2=OA2-（OC-CD）2，即202=AO2-（AO-8）2，
    解得AO=29m．即圆弧半径为29m．
    ∴这钢梁圆弧的半径是为29m．
    故选B．

    点评 本题考查了垂径定理和勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．先化简再求值：3a2-2（2a2-a）+2（a2-3a+1），其中a=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．为了鼓励市民节约用水，某市自来水公司对每户用水量进行了分段计费，每户每月用水量在规定吨数以下的收费标准相同，规定吨数以上的超过部分收费相同．如表是小明家1-4月用水量和交费情况：
    月份1234
    用水量（吨）681215
    费用（元）12162837
    （1）自来水公司规定用水量为8吨，规定用量的收费标准是2元/吨，超过部分收费3元/吨．
    （2）若小明家5月份用水25吨，则应缴多少元水费？
    （3）若小明6月份缴水费43元，则6月份他们家用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，在△AOC和△BOC中，若∠AOC=∠BOC，添加一个条件AO=BO，使得△AOC≌△BOC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知an=$\frac{1}{（n+1）^{2}}$（n=1，2，3，…），我们又定义b1=2（1-a1），b2=2（1-a1）（1-a2），…，bn=2（1-a1）（1-a2）…（1-an），则通过计算b1，b2…，bn，则b2014=$\frac{2016}{2015}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

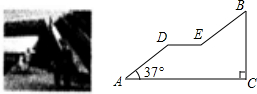    1．如图，城市人行天桥的引桥由楼梯AD、EB和一段水平平台DE构成，AD与EB互相平行并且与地面成37°角．已知引桥的高BC=6m，引桥的水平跨度AC=12m．
    （1）求两段楼梯AD、EB的总长度；
    （2）求水平平台DE的长．
    【参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75】

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）计算：（-3）2+|-2|-20150-$\sqrt{9}$+（$\frac{1}{2}$）-2
    （2）解不等式组：$\left\{\begin{array}{l}{4x-3＜3（2x+1）}\\{\frac{3}{2}x-1≤5-\frac{1}{2}x}\end{array}\right.$并在数轴上把解集表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

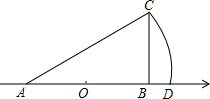    5．如图，数轴上点A表示的数是-1，原点O是线段AB的中点，∠BAC=30°，∠ABC=90°，以点A为圆心，AC为半径画弧，交数轴于点D，则点D表示的数是（　　）
    A．$\frac{2\sqrt{3}}{3}-1$B．$\frac{2\sqrt{3}}{3}$C．$\frac{4\sqrt{3}}{3}$D．$\frac{4\sqrt{3}}{3}-1$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．目前在成华区居住的常住人口约为96万，将数据96万（即960000）用科学记数法表示为（　　）
    A．9.6×10B．96×104C．9.6×105D．9.6×106

    查看答案和解析>>

    同步练习册答案