
【题目】下列边长为a的正多边形与边长为a的正方形组合起来,不能镶嵌成平面的是( )
(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形
A. (1)(2)B. (2)(3)C. (1)(3)D. (1)(4)
【答案】B
【解析】
由镶嵌的条件知,在一个顶点处各个内角和为360°,据此解答即可.
解:①正三角形的每个内角是60°,正方形的每个内角是90°.∵3×60°+2×90°=360°,∴能镶嵌平面;
②正方形的每个内角是90°,正五边形每个内角是180°360°÷5=108°,90m+108n=360°,显然n取任何正整数时,m不能得正整数,不能镶嵌平面;
③正方形的每个内角是90°,正六边形的每个内角是120度.90m+120n=360°,m=4![]() ,显然n取任何正整数时,m不能得正整数,不能镶嵌平面;
,显然n取任何正整数时,m不能得正整数,不能镶嵌平面;
④正方形的每个内角是90°,正八边形的每个内角为180°360°÷8=135°,∵90°+2×135°=360°,∴能镶嵌平面.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,则树高AB=( )m.
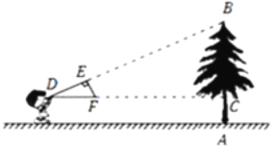
A. 3.5B. 4C. 4.5D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某街道路边有相距10m、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面A处测得路灯PQ的顶端仰角为14°,向前行走25m到达B处,在地面测得路灯MN的顶端仰角为24.3°,已知点A,B,Q,N在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到0.1m.参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin24.3°≈0.41,cos24.3°≈0.91,tan24.3°≈0.45)
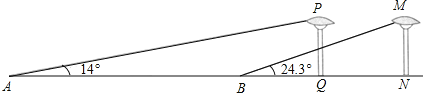
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.

(1)如图①,若∠BAC=23°,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要把破残的圆片复制完整,已知弧上三点A、B、C.
(1)用尺规作图法,找出弧BAC所在圆的圆心O;(保留作图痕迹,不写作法)
(2)设△ABC为等腰三角形,底边BC=10 cm,腰AB=6 cm,求圆片的半径R;(结果保留根号)
(3)若在(2)题中的R满足n<R<m(m、n为正整数),试估算m和n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-2x+1=0.
(1)若方程有两个实数根,求m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2-x1-x2=![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是矩形ABCD的边AD延长线上一点,以AM为直径的⊙O交矩形对角线AC于点F,在线段CD上取一点E,连接EF,使EC=EF.

(1)求证:EF是⊙O的切线;
(2)若cos∠CAD=![]() ,AF=6,MD=2,求FC的长.
,AF=6,MD=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点分别是A(﹣3,2)B(0,4)C(0,2).
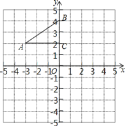
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连接AB1,BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com