
分析 首先把分式的分子和分母分解因式,把除法转化为乘法,然后约分即可化简,然后代入适当的数即可求解.
解答 解:$\frac{2x-6}{{x}^{2}-4x+4}$$•\frac{{x}^{2}+6x+9}{4x-12}$÷$\frac{x+3}{x-2}$
=$\frac{2(x-3)}{(x-2)^{2}}$•$\frac{(x+3)^{2}}{4(x-3)}$•$\frac{x-2}{x+3}$
=$\frac{x+3}{2(x-2)}$,
当x=0时,原式=$\frac{3}{-4}$=-$\frac{3}{4}$.
点评 本题考查了分式的化简求值,取喜爱的数代入求值时,要特注意原式及化简过程中的每一步都有意义.如果取x=0,则原式没有意义,因此,尽管0是大家的所喜爱的数,但在本题中却是不允许的.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
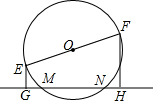 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com