
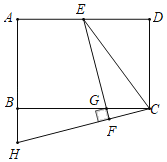
【题目】如图,在长方形ABCD中,点E是AD的中点,连接CE,将△CDE沿着CE翻折得到△CFE,EF交BC于点G,CF的延长线交AB的延长线于点H,若AH=25,BC=40,则FG=_____.
【答案】![]() .
.
【解析】
由矩形的性质得出∠A=∠D=90°,AD=BC=40,由点E是AD的中点,得出AE=DE=![]() AD=20,由折叠性质得FE=DE=20,∠EFC=∠D=90°,CF=CD,∠CEF=∠CED,则AE=EF,∠EFH=90°=∠A,连接EH,由HL证得Rt△AEH≌Rt△FEH,得出FH=AH=25,∠AEH=∠FEH,推出∠HEC=90°,设CD=x,则CH=25+x,由勾股定理得出EH2=AH2+AE2,CE2=DE2+CD2,CH2=E2+CE2,则CH2=AH2+AE2+DE2+CD2,即(25+x)2=252+202+202+x2,解得x=16,作EM⊥BC于M,则EM=CD=CF=16,CM=DE=20,由AAS证得△EMG≌△CFG,得出MG=FG,设EG=y,则MG=FG=20﹣y,在Rt△EMG中,由勾股定理得y2=162+(20﹣y)2,解得y=
AD=20,由折叠性质得FE=DE=20,∠EFC=∠D=90°,CF=CD,∠CEF=∠CED,则AE=EF,∠EFH=90°=∠A,连接EH,由HL证得Rt△AEH≌Rt△FEH,得出FH=AH=25,∠AEH=∠FEH,推出∠HEC=90°,设CD=x,则CH=25+x,由勾股定理得出EH2=AH2+AE2,CE2=DE2+CD2,CH2=E2+CE2,则CH2=AH2+AE2+DE2+CD2,即(25+x)2=252+202+202+x2,解得x=16,作EM⊥BC于M,则EM=CD=CF=16,CM=DE=20,由AAS证得△EMG≌△CFG,得出MG=FG,设EG=y,则MG=FG=20﹣y,在Rt△EMG中,由勾股定理得y2=162+(20﹣y)2,解得y=![]() ,即可得出结果.
,即可得出结果.
解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,AD=BC=40,
∵点E是AD的中点,
∴AE=DE=![]() AD=20,
AD=20,
由折叠性质得:FE=DE=20,∠EFC=∠D=90°,CF=CD,∠CEF=∠CED,
∴AE=EF,∠EFH=90°=∠A,
连接EH,如图所示:

在Rt△AEH和Rt△FEH中,![]() ,
,
∴Rt△AEH≌Rt△FEH(HL),
∴FH=AH=25,∠AEH=∠FEH,
∴∠HEC=∠FEH+∠CEF=![]() ∠AEF+
∠AEF+![]() ∠DEF=
∠DEF=![]() ×180°=90°,
×180°=90°,
设CD=x,则CH=25+x,
∵EH2=AH2+AE2,CE2=DE2+CD2,CH2=HE2+CE2,
∴CH2=AH2+AE2+DE2+CD2,
即(25+x)2=252+202+202+x2,
整理得:50x=800,
解得:x=16,
作EM⊥BC于M,
则EM=CD=CF=16,CM=DE=20,
在△EMG和△CFG中, ,
,
∴△EMG≌△CFG(AAS),
∴MG=FG,
设EG=y,则MG=FG=20﹣y,
在Rt△EMG中,由勾股定理得:y2=162+(20﹣y)2,
解得:y=![]() ,
,
∴FG=20﹣![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明周末要乘坐公交车到植物园游玩,从地图上查找路线发现,几条线路都需要换乘一次.在出发站点可选择空调车A、空调车B、普通车a,换乘站点可选择空调车C,普通车b、普通车c,且均在同一站点换乘.空调车投币2元,普通车投币1元.
(1)求小明在出发站点乘坐空调车的概率;
(2)求小明到达植物园恰好花费3元公交费的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,CD⊥BC,已知AB=5,BC=6,cosB=![]() .点O为BC边上的动点,以O为圆心,BO为半径的⊙O交边AB于点P.
.点O为BC边上的动点,以O为圆心,BO为半径的⊙O交边AB于点P.
(1)设OB=x,BP=y,求y与x的函数关系式,并写出函数定义域;
(2)当⊙O与以点D为圆心,DC为半径⊙D外切时,求⊙O的半径;
(3)连接OD、AC,交于点E,当△CEO为等腰三角形时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2.若S=3,则S1+S2的值为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上弧BF的中点,CD⊥AF,垂足为D,AB、DC的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com