
【题目】如图,梯形ABCD中,AD∥BC,CD⊥BC,已知AB=5,BC=6,cosB=![]() .点O为BC边上的动点,以O为圆心,BO为半径的⊙O交边AB于点P.
.点O为BC边上的动点,以O为圆心,BO为半径的⊙O交边AB于点P.
(1)设OB=x,BP=y,求y与x的函数关系式,并写出函数定义域;
(2)当⊙O与以点D为圆心,DC为半径⊙D外切时,求⊙O的半径;
(3)连接OD、AC,交于点E,当△CEO为等腰三角形时,求⊙O的半径.

【答案】(1)y=![]() x(0<x≤
x(0<x≤![]() );(2)1.8;(3)当△CEO为等腰三角形时,⊙O的半径为3或4.
);(2)1.8;(3)当△CEO为等腰三角形时,⊙O的半径为3或4.
【解析】
(1)首先作OM⊥BD,即可满足垂径定理,在直角△OBM中求得BM的长,即可求得BP;
(2)连接OD.作AN⊥BC,根据三角函数即可求得CD的长,根据两圆相外切时,圆心距等于半径的和即可得到一个关于半径长的一个方程,即可求得半径长;
(3)当△CEO为等腰三角形时,利用当EO=EC时,当CE=CO时,分别求得圆的半径.
(1)作OM⊥BP,
则BP=2BM.
在直角△BMO中,
cosB=![]() =
=![]() .
.
∴BM=OBcosB=![]() .
.
则BP=2BM=![]() .
.
∴函数的解析式是:y=![]() x(0<x≤
x(0<x≤![]() );
);
(2)连接OD.作AN⊥BC.
∵在直角△ABN中,cosB=![]() =
=![]() .
.
∴BN=ABcosB=5×![]() =3.
=3.
则AN=CD=4.
在直角△OCD中,OC=BC﹣OB=6﹣x,CD=4.
则OD=![]() .
.
当两圆相切时:![]() =x+4
=x+4
解得:x=1.8;
(3)在Rt△ACD中,AC=5,设⊙O的半径为x,
当EO=EC时,∠EOC=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠EOC,
∴AB∥OD,
又∵AD∥BC,
∴OB=AD=3,
∴⊙O的半径为3,
当OE=OC时,∠ECO=∠CEO,
∵AD∥BC,
∴∠DAE=∠ECO,
∵∠AED=∠CEO,∴∠DAE=∠AED,
∴AD=DE=3,
∴OD=OE+DE=6﹣x+3=9﹣x,
在Rt△OCD中,
∵CD2+OC2=OD2,
∴42+(6﹣x)2=(9﹣x)2,
解得:x=![]() (不合题意舍去)
(不合题意舍去)
当CE=CO时,∠CEO=∠COE,
∵AD∥BC,
∴∠ADE=∠COE,
∵∠AED=∠CEO,
∴∠AED=∠ADE,
∴AD=AE=3,
∵CE+AE=AC,
∴6﹣x+3=5,
∴x=4,
∴⊙O的半径为4.
综上所述,当△CEO为等腰三角形时,⊙O的半径为3或4.



科目:初中数学 来源: 题型:
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某计算机中有![]() 、
、![]() 、
、![]() 三个按键,以下是这三个按键的功能.
三个按键,以下是这三个按键的功能.
(1).![]() :将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下
:将荧幕显示的数变成它的正平方根,例如:荧幕显示的数为49时,按下![]() 后会变成7.
后会变成7.
(2).![]() :将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下
:将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下![]() 后会变成0.04.
后会变成0.04.
(3).![]() :将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下
:将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下![]() 后会变成36.
后会变成36.
若荧幕显示的数为100时,小刘第一下按![]() ,第二下按
,第二下按![]() ,第三下按
,第三下按![]() ,之后以
,之后以![]() 、
、![]() 、
、![]() 的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )
的顺序轮流按,则当他按了第100下后荧幕显示的数是多少( )

A. 0.01 B. 0.1 C. 10 D. 100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=13,点A、B的坐标分别为(1,0),(6,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣4上时,线段BC扫过的面积为( )

A.84B.80C.91D.78
查看答案和解析>>
科目:初中数学 来源: 题型:
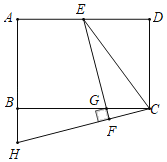
【题目】如图,在长方形ABCD中,点E是AD的中点,连接CE,将△CDE沿着CE翻折得到△CFE,EF交BC于点G,CF的延长线交AB的延长线于点H,若AH=25,BC=40,则FG=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() 与x轴、y轴分别相交于点A、B,直线l2与直线y=﹣
与x轴、y轴分别相交于点A、B,直线l2与直线y=﹣![]() x平行,且与直线l1相交于点B,与x轴交于点C.
x平行,且与直线l1相交于点B,与x轴交于点C.

(1)求点C坐标;
(2)若点P是y轴右侧直线l1上一动点,点Q是直线l2上一动点,点D(﹣2![]() ,6
,6![]() ),求当S△PBC=S四边形AOBD时,点P的坐标,并求出此时,PQ+DQ的最小值;
),求当S△PBC=S四边形AOBD时,点P的坐标,并求出此时,PQ+DQ的最小值;
(3)将△AOB沿着直线l2平移,平移后记为△A1O1B1,直线O1B1交11于点M,直线A1B1交x轴于点N,当△B1MN是等腰三角形时,求点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《实数》内容时,我们估算带有根号的无理数的近似值时,经常使用“逐步逼近”的方法来实现的.“逐步逼近”是数学思维方法的一种重要形式,主要通过构造“拟对象”、逐步扩充元素、逐步扩充范围、放缩逼近、合力逼近等方式解决问题.
例如:估算![]() 的近似值时,利用“逐步逼近”法可以得出
的近似值时,利用“逐步逼近”法可以得出![]() .请你根据阅读内容回答下列问题:
.请你根据阅读内容回答下列问题:
(1)![]() 介于连续的两个整数
介于连续的两个整数![]() 和
和![]() ,且
,且![]() ,那么
,那么![]() ______,
______,![]() ______;
______;
(2)![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
(3)已知![]() 的小数部分为
的小数部分为![]() ,
,![]() 的小数部分为
的小数部分为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长x与等边△ABC的周长y的关系.

(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是 ; 此时![]() = ;
= ;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想( I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com