
【题目】在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长x与等边△ABC的周长y的关系.

(1)如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是 ; 此时![]() = ;
= ;
(2)如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想( I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.
(3)如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.
【答案】(1)BM+NC=MN;![]() ;(2)成立:BM+NC=MN;(3)BM+MN=NC.证明见解析.
;(2)成立:BM+NC=MN;(3)BM+MN=NC.证明见解析.
【解析】
(1)由DM=DN,∠MDN=60°,可证得△MDN是等边三角形,又由△ABC是等边三角形,CD=BD,易证得Rt△BDM≌Rt△CDN,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系 BM+NC=MN,此时![]() ;
;
(2)在CN的延长线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;
(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC-BM=MN.
解:(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.
此时![]() .
.
理由:∵DM=DN,∠MDN=60°,
∴△MDN是等边三角形,
∵△ABC是等边三角形,
∴∠A=60°,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠MBD=∠NCD=90°,
∵DM=DN,BD=CD,
∴Rt△BDM≌Rt△CDN,
∴∠BDM=∠CDN=30°,BM=CN,
∴DM=2BM,DN=2CN,
∴MN=2BM=2CN=BM+CN;
∴AM=AN,
∴△AMN是等边三角形,
∵AB=AM+BM,
∴AM:AB=2:3,
∴![]() ;
;
(2)猜想:结论仍然成立.
证明:在NC的延长线上截取CM1=BM,连接DM1.
∵∠MBD=∠M1CD=90°,BD=CD,
∴△DBM≌△DCM1,
∴DM=DM1,∠MBD=∠M1CD,M1C=BM,
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N=M1C+NC=BM+NC,
∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,
∴![]() ;
;

(3)证明:在CN上截取CM1=BM,连接DM1.
可证△DBM≌△DCM1,
∴DM=DM1,
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN,
∴MN=M1N,
∴NC-BM=MN.


科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,CD⊥BC,已知AB=5,BC=6,cosB=![]() .点O为BC边上的动点,以O为圆心,BO为半径的⊙O交边AB于点P.
.点O为BC边上的动点,以O为圆心,BO为半径的⊙O交边AB于点P.
(1)设OB=x,BP=y,求y与x的函数关系式,并写出函数定义域;
(2)当⊙O与以点D为圆心,DC为半径⊙D外切时,求⊙O的半径;
(3)连接OD、AC,交于点E,当△CEO为等腰三角形时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得x分,答错或不答扣y分,下表记录了其中两个参赛者的得分情况:
参赛者 | 答对题数 | 答错或不答题数 | 得分 |
A | 18 | 2 | 104 |
B | 13 | 7 | 64 |
(1)求出x和y的值;
(2)若参赛者C的得分要超过80分,则他至少要答对多少道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且量得BF=12cm.求:(1)AD的长;(2)DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1, ![]() 的顶点都在正方形网格的格点(网格线的交点)上.
的顶点都在正方形网格的格点(网格线的交点)上.

(1)请在图中的网格平面内画出平面直角坐标系,使点![]() 坐标为(7,6),点
坐标为(7,6),点![]() 坐标为(2,1);
坐标为(2,1);
(2)在(1)的条件下,
①请画出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
②点![]() 是边
是边![]() 上的一个动点,连接
上的一个动点,连接![]() ,则
,则![]() 周长的最小值为 .
周长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上弧BF的中点,CD⊥AF,垂足为D,AB、DC的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+2S2+2S3+S4=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
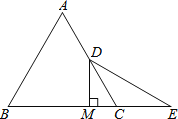
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
(1)求证:M是BE的中点.
(2)若CD=1,DE=![]() ,求△ABD的周长.
,求△ABD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com