
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线.
(2)当OA=3,AE=4时,求BC的长度.

(1)证明见解析;(2)10.
【解析】
试题分析:(1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)利用圆周角定理和垂径定理推知OE∥BC,所以根据平行线分线段成比例求得BC的长度即可.
试题解析:(1)证明:如图,连接OD.
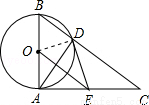
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
 ,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)【解析】
如图,在△OAE中,∠OAE=90°,OA=3,AE=4,
∴由勾股定理易求OE=5.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO,
又∵AE=DE,
∴OE⊥AD,
∴OE∥BC,
∴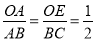 .
.
BC=2OE=10,即BC的长度是10.
考点:切线的判定.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:选择题
永州的文化底蕴深厚,永州人民的生活健康向上,如瑶族长鼓舞,东安武术,宁远举重等,下面的四幅简笔画是从永州的文化活动中抽象出来的,其中是轴对称图形的是( )

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南常德卷)数学(解析版) 题型:填空题
下列关于反比例函数y= 的三个结论:
的三个结论:
①它的图象经过点(7,3);
②它的图象在每一个象限内,y随x的增大而减小;
③它的图象在二、四象限内.
其中正确的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com