
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 不能唯一确定 |
分析 设△ABC中,∠A=30°,因为题意表述有一边是另一边的2倍,没有具体指出哪两条边,所以需要讨论:①a=2b,利用大边对大角的知识可得出∠B<∠A,利用不等式可表示出C的角度范围;②b=2c,利用大边对大角的知识可得出∠C<∠A,利用不等式可表示出B的角度范围;③c=2a,利用直角三角中,30°角所对的边等于斜边的一半,可判断∠C为90°.综合三种情况再结合选项即可做出选择.
解答 解:设△ABC中,∠A=30°,
①若a=2b,则∠B<∠A(大边对大角),
∴∠C=180°-∠A-∠B>180°-2∠A=120°,即∠C为钝角,
∴△ABC是钝角三角形.
②若b=2c,a2=b2+c2-2bccosA=5c2-2$\sqrt{3}$c2,$\frac{{a}^{2}}{{c}^{2}}$=5-2$\sqrt{3}$>1,可得a>c,
∴∠C<∠A(大边对大角),
∴∠B=180°-∠A-∠C>180°-2∠A=120°,即∠B为钝角,
∴△ABC是钝角三角形;
③c=2a,在直角三角形中30°所对的边为斜边的一半,可得∠C=90°,即△ABC是直角三角形.
综上可得△ABC可为直角三角形、钝角三角形,不能为锐角三角形.
故选D.
点评 本题考查三角形的边角关系,解答本题需要掌握在三角形中“大边对应大角”,及直角三角形的性质:在直角三角形中30°所对的边为斜边的一半,难度较大,注意分类讨论.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{\frac{3}{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
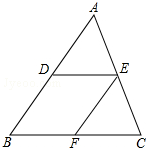 如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.试问当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.试问当△ABC满足什么条件时,四边形DBFE是菱形?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com