
【题目】如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.

(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)
【解析】试题分析:(1)根据折叠得出AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,在Rt△ABC中,根据勾股定理求出AC,在Rt△PCD1中,根据勾股定理得出方程,求出即可;
(2)连接PE,求出BE=CE=1,在Rt△ABE中,根据勾股定理求出AE,求出AD1=AD=2,PD=PD1=x,D1E=![]() ﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;
﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;
(3)分为两种情况:当0<x≤2时,y=x;当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,求出AF=PF,作PG⊥AB于G,设PF=AF=a,在Rt△PFG中,由勾股定理得出方程(x﹣a)2+22=a2,求出a即可.
试题解析:解:(1)如图1,∵由题意得:△ADP≌△AD1P,∴AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,∵直线AD1过C,∴PD1⊥AC,在Rt△ABC中,AC=![]() =
=![]() ,CD1=
,CD1=![]() ﹣2,在Rt△PCD1中,PC2=PD12+CD12,即(3﹣x)2=x2+(
﹣2,在Rt△PCD1中,PC2=PD12+CD12,即(3﹣x)2=x2+(![]() ﹣2)2,解得:x=
﹣2)2,解得:x=![]() ,∴当x=
,∴当x=![]() 时,直线AD1过点C;
时,直线AD1过点C;

(2)如图2,连接PE,∵E为BC的中点,∴BE=CE=1,在Rt△ABE中,AE=![]() =
=![]() ,∵AD1=AD=2,PD=PD1=x,∴D1E=
,∵AD1=AD=2,PD=PD1=x,∴D1E=![]() ﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,x2+(
﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,x2+(![]() ﹣2)2=(3﹣x)2+12,解得:x=
﹣2)2=(3﹣x)2+12,解得:x=![]() ,∴当x=
,∴当x=![]() 时,直线AD1过BC的中点E;
时,直线AD1过BC的中点E;

(3)①如图3,当0<x≤2时,y=x;

②如图4,当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,∵AB∥CD,∴∠1=∠2,∵∠1=∠3(根据折叠),∴∠2=∠3,∴AF=PF,作PG⊥AB于G,设PF=AF=a,由题意得:AG=DP=x,FG=x﹣a,在Rt△PFG中,由勾股定理得:(x﹣a)2+22=a2,解得:a=![]() ,所以y=
,所以y=![]() =
=![]() .
.
综合上述,  .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】你知道吗,即使被动吸烟也大大危害健康、国家规定在公众场所实行“禁烟”,为配合“禁烟”行动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查,征求市民的意见,并将调查结果整理后制成了如下统计图:
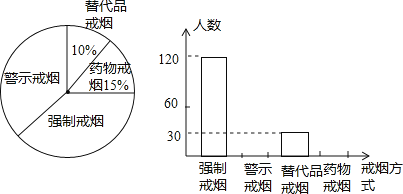
根据统计图解答:
(1)同学们一共随机调查了多少人?
(2)请你把统计图补充完整;
(3)假定该社区有5000人,请估计该社区大约有多少人支持“警示戒烟”这种方式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.求证:
(1)△BAD≌△CAE;
(2)BD⊥CE

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划组织![]() 名师生租乘汽车外出研学一天,需租用大巴、中巴共
名师生租乘汽车外出研学一天,需租用大巴、中巴共![]() 辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐
辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐![]() 名乘客,中巴每辆可乘坐
名乘客,中巴每辆可乘坐![]() 名乘客.
名乘客.
(1)求该校应租用大巴、中巴各多少辆?(请用含![]() 的代数式表示)
的代数式表示)
(2)若每辆大巴租金是![]() 元/天,中巴租金是
元/天,中巴租金是![]() 元/天,若租金不能超过
元/天,若租金不能超过![]() 元,则应租用大巴、中巴各多少辆?
元,则应租用大巴、中巴各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=x﹣![]() 的图象和性质.
的图象和性质.
小石根据学习函数的经验,对此函数的图象和性质进行了探究.
下面是小石的探究过程,请补充完整:
(1)函数的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值,
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | ﹣1 | 1 |
|
| ﹣ | ﹣ | m | 1 |
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出此函数的图象;
(4)进一步探究,结合函数的图象,写出此函数的性质(一条即可): .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以ABCD 的四条边为边,分别向外作正方形,连结 EF,GH,IJ,KL.如果ABCD 的 面积为 8,则图中阴影部分四个三角形的面积和为( )

A.8B.12C.16D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个以点O为圆心的同心圆,
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com