
ĄūĖâÄŋĄŋČįÍž1ĢŽÔÚÖą―ĮŨøąęÏĩÖÐĢŽŌŅÖŠĩãAĢĻ0ĢŽ2ĢĐĄĒĩãBĢĻ-2ĢŽ0ĢĐĢŽđýĩãBšÍÏßķÎOAĩÄÖÐĩãCŨũÖąÏßBCĢŽŌÔÏßķÎBCΊąßÏōÉÏŨũÕý·―ÐÎBCDE.
ĢĻ1ĢĐĖîŋÕĢšĩãDĩÄŨøąęΊ_________ĢŽĩãEĩÄŨøąęΊ_______________.
ĢĻ2ĢĐČôÅŨÎïÏß![]() ūđýAĄĒDĄĒEČýĩãĢŽĮóļÃÅŨÎïÏßĩÄ―âÎöĘ―.
ūđýAĄĒDĄĒEČýĩãĢŽĮóļÃÅŨÎïÏßĩÄ―âÎöĘ―.
ĢĻ3ĢĐČôÕý·―ÐΚÍÅŨÎïÏßūųŌÔÃŋÃë![]() ļöĩĨÎŧģĪķČĩÄËŲķČŅØÉäÏßBCÍŽĘąÏōÉÏÆ―ŌÆĢŽÖąÖÁÕý·―ÐÎĩÄķĨĩãEÂäÔÚ
ļöĩĨÎŧģĪķČĩÄËŲķČŅØÉäÏßBCÍŽĘąÏōÉÏÆ―ŌÆĢŽÖąÖÁÕý·―ÐÎĩÄķĨĩãEÂäÔÚ![]() ÖáÉÏĘąĢŽÕý·―ÐΚÍÅŨÎïÏßūųÍĢÖđÔËķŊ.
ÖáÉÏĘąĢŽÕý·―ÐΚÍÅŨÎïÏßūųÍĢÖđÔËķŊ.
ĒŲÔÚÔËķŊđýģĖÖÐĢŽÉčÕý·―ÐÎÂäÔÚyÖáÓŌēāēŋ·ÖĩÄÃæŧýΊ![]() ĢŽĮó
ĢŽĮó![]() đØÓÚÆ―ŌÆĘąžä
đØÓÚÆ―ŌÆĘąžä![]() ĢĻÃëĢĐĩÄšŊĘýđØÏĩĘ―ĢŽēĒÐīģöÏāÓĶŨÔąäÁŋ
ĢĻÃëĢĐĩÄšŊĘýđØÏĩĘ―ĢŽēĒÐīģöÏāÓĶŨÔąäÁŋ![]() ĩÄČĄÖĩ·ķΧ.
ĩÄČĄÖĩ·ķΧ.
ĒÚÔËķŊÍĢÖđĘąĢŽĮóÅŨÎïÏßĩÄķĨĩãŨøąę.
Ąūīð°ļĄŋĢĻ1ĢĐDĩÄŨøąęΊĢĻ-1ĢŽ3ĢĐĢŽEĩÄŨøąęΊĢĻ-3ĢŽ2ĢĐĢŧ
ĢĻ2ĢĐÅŨÎïÏßĩÄ―âÎöĘ―ÎŠ![]() Ģŧ
Ģŧ
ĢĻ3ĢĐĒŲSÓëxĩÄšŊĘýđØÏĩĘ―ÎŠĢš
ĩą0ĢžtĄÜ![]() Ęą, S=5
Ęą, S=5![]()
ĩą![]() ĢžtĄÜ1ĘąĢŽS=5t
ĢžtĄÜ1ĘąĢŽS=5t![]()
ĩą1ĢžtĄÜ![]() ĘąĢŽS=-5t2+15t
ĘąĢŽS=-5t2+15t![]()
ĒÚÅŨÎïÏßĩÄķĨĩãŨøąęĘĮĢĻ![]() ĢŽ
ĢŽ ![]() ĢĐ.
ĢĐ.
Ąū―âÎöĄŋĢĻ1ĢĐDĢĻ-1ĢŽ3ĢĐĄĒEĢĻ-3ĢŽ2ĢĐĢĻ2·ÖĢĐ
ĢĻ2ĢĐÅŨÎïÏßūđýĢĻ0ĢŽ2ĢĐĄĒĢĻ-1ĢŽ3ĢĐĄĒĢĻ-3ĢŽ2ĢĐĢŽÔō
![]()
―âĩÃ ![]()
Ąā![]()
ĢĻ3ĢĐĒŲĩąĩãDÔËķŊĩ―yÖáÉÏĘąĢŽt=![]() .
.
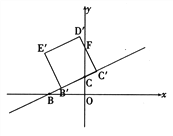
ĩą0ĢžtĄÜ![]() ĘąĢŽČįÓŌÍž
ĘąĢŽČįÓŌÍž
ÉčDĄäCĄä―ŧyÖáÓÚĩãF
ĄßtanĄÏBCO= ![]() =2,Ó֥ߥÏBCO=ĄÏFCCĄä
=2,Ó֥ߥÏBCO=ĄÏFCCĄä
ĄātanĄÏFCCĄä=2, žī![]() =2
=2
ĄßCCĄä= ![]() t,ĄāFCĄä=2
t,ĄāFCĄä=2![]() t.
t.
ĄāSĄũCCĄäF =![]() CCĄäĄĪFCĄä=
CCĄäĄĪFCĄä= ![]() tĄÁ
tĄÁ![]() t=5 t2
t=5 t2
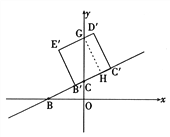 ĩąĩãBÔËķŊĩ―ĩãCĘąĢŽt=1.ĩą
ĩąĩãBÔËķŊĩ―ĩãCĘąĢŽt=1.ĩą![]() ĢžtĄÜ1ĘąĢŽČįÓŌÍž
ĢžtĄÜ1ĘąĢŽČįÓŌÍž
ÉčDĄäEĄä―ŧyÖáÓÚĩãGĢŽđýGŨũGHĄÍBĄäCĄäÓÚH.
ÔÚRtĄũBOCÖÐĢŽBC= ![]()
ĄāGH= ![]() ,ĄāCH=
,ĄāCH=![]() GH=
GH= ![]()
ĄßCCĄä=![]() t,ĄāHCĄä=
t,ĄāHCĄä=![]() t-
t-![]() ,ĄāGDĄä=
,ĄāGDĄä=![]() t-
t-![]()
ĄāSĖÝÐÎCCĄäDĄäG =![]() (
(![]() t-
t-![]() +
+ ![]() t)
t) ![]() =5t-
=5t-![]()
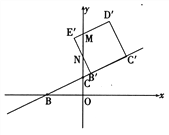 ĩąĩãEÔËķŊĩ―yÖáÉÏĘąĢŽt=
ĩąĩãEÔËķŊĩ―yÖáÉÏĘąĢŽt=![]() .
.
ĩą1ĢžtĄÜ![]() ĘąĢŽČįÓŌÍžËųĘū
ĘąĢŽČįÓŌÍžËųĘū
ÉčDĄäEĄäĄĒEĄäBĄä·Öąð―ŧyÖáÓÚĩãMĄĒN
ĄßCCĄä=![]() tĢŽBĄäCĄä=
tĢŽBĄäCĄä=![]() ,
,
ĄāCBĄä=![]() t-
t-![]() ,ĄāBĄäN=2CBĄä=
,ĄāBĄäN=2CBĄä=![]() t-
t-![]()
ĄßBĄäEĄä=![]() ,ĄāEĄäN=BĄäEĄä-BĄäN=
,ĄāEĄäN=BĄäEĄä-BĄäN=![]() -
-![]() t
t
ĄāEĄäM=![]() EĄäN=
EĄäN=![]() (
(![]() -
-![]() t)
t)
ĄāSĄũMNEĄä =![]() (
(![]() -
-![]() t)ĄĪ
t)ĄĪ![]() (
(![]() -
-![]() t)=5t2-15t+
t)=5t2-15t+![]()
ĄāSÎåąßÐÎBĄäCĄäDĄäMN =SÕý·―ÐÎBĄäCĄäDĄäEĄä -SĄũMNEĄä =![]() (5t2-15t+
(5t2-15t+![]() )=-5t2+15t-
)=-5t2+15t-![]()
ŨÛÉÏËųĘöĢŽSÓëxĩÄšŊĘýđØÏĩĘ―ÎŠĢš
ĩą0ĢžtĄÜ![]() Ęą, S=5
Ęą, S=5![]()
ĩą![]() ĢžtĄÜ1ĘąĢŽS=5t
ĢžtĄÜ1ĘąĢŽS=5t![]()
ĩą1ĢžtĄÜ![]() ĘąĢŽS=-5t2+15t
ĘąĢŽS=-5t2+15t![]()
ĒÚĩąĩãEÔËķŊĩ―ĩãEĄäĘąĢŽÔËķŊÍĢÖđ.ČįÏÂÍžËųĘū
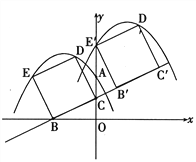 ĄßĄÏCBĄäEĄä=ĄÏBOC=90ĄãĢŽĄÏBCO=ĄÏBĄäCEĄä
ĄßĄÏCBĄäEĄä=ĄÏBOC=90ĄãĢŽĄÏBCO=ĄÏBĄäCEĄä
ĄāĄũBOCĄŨĄũEĄäBĄäC
Ąā![]()
ĄßOB=2ĢŽBĄäEĄä=BC=![]()
Ąā![]()
ĄāCEĄä=![]()
ĄāOEĄä=OC+CEĄä=1+![]() =
=![]()
ĄāEĄäĢĻ0ĢŽ![]() ĢĐ
ĢĐ
ÓÉĩãEĢĻ-3ĢŽ2ĢĐÔËķŊĩ―ĩãEĄäĢĻ0ĢŽ ![]() ĢĐ,ŋÉÖŠÕûĖõÅŨÎïÏßÏōÓŌÆ―ŌÆÁË3ļöĩĨÎŧĢŽÏōÉÏÆ―ŌÆÁË
ĢĐ,ŋÉÖŠÕûĖõÅŨÎïÏßÏōÓŌÆ―ŌÆÁË3ļöĩĨÎŧĢŽÏōÉÏÆ―ŌÆÁË![]() ļöĩĨÎŧ.
ļöĩĨÎŧ.
Ąß![]() =
= ![]()
ĄāÔÅŨÎïÏßķĨĩãŨøąęΊĢĻ![]() ĢŽ
ĢŽ ![]() ĢĐ
ĢĐ
ĄāÔËķŊÍĢÖđĘąĢŽÅŨÎïÏßĩÄķĨĩãŨøąęΊĢĻ![]() ĢŽ
ĢŽ ![]() ĢĐ
ĢĐ


 ÔÄķÁŋėģĩÏĩÁÐīð°ļ
ÔÄķÁŋėģĩÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĄ°ŅôđâĖåÓýĄąÔËķŊđØšõÃŋļöŅ§ÉúÎīĀīĩÄÐŌļĢÉúŧîĢŽ―ņÄęÎåÔÂĢŽÎŌĘÐÄģÐĢŋŠÕđÁËŌÔĄ°ŅôđâĖåÓýÎŌĘĮđÚūüĄąÎŠÖũĖâĩÄŌŧ·ÖÖÓÏÞĘąĖøÉþąČČüĢŽŌŠĮóÃŋļö°āŅĄ2Đ3ÃûŅĄĘÖēÎČüĢŽÏÖ―Ŧ80ÃûŅĄĘÖąČČüģÉžĻĢĻĩĨÎŧĢšīÎ/·ÖÖÓĢĐ―øÐÐÍģžÆĢŪŧæÖÆģÉÆĩĘý·ÖēžÖą·―ÍžĢŽČįÍžËųĘūĢŪ
ĢĻ1ĢĐÍžÖÐaÖĩΊĄĄĄĄĢŪ
ĢĻ2ĢĐ―ŦĖøÉþīÎĘýÔÚ160ĄŦ190ĩÄŅĄĘÖŌĀīΞĮΊA1ĄĒA2ĄĒĄAnĢŽīÓÖÐËæŧúģéČĄÁ―ÃûŅĄĘÖŨũūŅé―ŧÁũĢŽĮëÓÃĘũŨīŧōÁÐąí·ĻĮóĮĄšÃģéČĄĩ―ĩÄŅĄĘÖA1šÍA2ĩÄļÅÂĘĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠČįÍžĢŽÖąÏßABĄĒCDÏā―ŧÓÚOĢŽĄÏAOC=50ĄãĢŽOEÆ―·ÖĄÏDOBĢŽĮóĄÏCOEĩÄķČĘýĢŪ 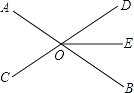
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽģĪ·―ÐÎAOBCÔÚÖą―ĮŨøąęÏĩÖÐĢŽĩãAÔÚyÖáÉÏĢŽĩãBÔÚxÖáÉÏĢŽŌŅÖŠĩãCĩÄŨøąęĘĮĢĻ8ĢŽ4ĢĐĢŪ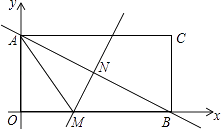
ĢĻ1ĢĐĮóķÔ―ĮÏßABËųÔÚÖąÏßĩÄšŊĘýđØÏĩĘ―Ģŧ
ĢĻ2ĢĐķÔ―ĮÏßABĩÄīđÖąÆ―·ÖÏßMN―ŧxÖáÓÚĩãMĢŽÁŽ―ÓAMĢŽĮóÏßķÎAMĩÄģĪĢŧ
ĢĻ3ĢĐČôĩãPĘĮÖąÏßABÉÏĩÄŌŧļöķŊĩãĢŽĩąĄũPAMĩÄÃæŧýÓëģĪ·―ÐÎOABCĩÄÃæŧýÏāĩČĘąĢŽĮóĩãPĩÄŨøąęĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
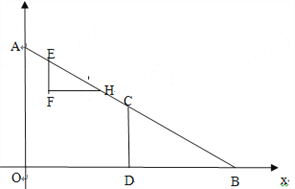
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÖą―ĮŨøąęÏĩÖÐĢŽĩãA(0ĢŽ6)ĢŽB(8ĢŽ0)ĢŽĩãCĘĮÏßķÎABĩÄÖÐĩãĢŽCDĄÍOB―ŧOBÓÚDĢŽRtĄũEFHĩÄÐąąßEHÔÚÉäÏßABÉÏĢŽķĨĩãFÔÚÉäÏßABĩÄŨóēāĢŽEFĄÎOAĢŽĩãEīÓĩãAģö·ĒĢŽŌÔÃŋÃë1ļöĩĨÎŧĩÄËŲķČÏōBÔËķŊĢŽĩ―ĩãBÍĢÖđĢŽAE=EFĢŽÔËķŊĘąžäΊtĢĻsĢĐ.
ĢĻ1ĢĐÔÚRtĄũEFHÖÐĢŽEF= ĢŽEH= ,ĩãFŨøąęΊĢĻ ĢŽ ĢĐĢĻÓÚŽtĩÄīúĘýĘ―ąíĘūĢĐ
ĢĻ2ĢĐtΊšÎÖĩĘąĢŽHÓëCÖØšÏĢŋ
ĢĻ3ĢĐÉčĄũEFHÓëĄũCDBÖØĩþēŋ·ÖÍžÐÎĩÄÃæŧýΊS(S>0)ĢŽĮóSÓëtĩÄšŊĘýđØÏĩĘ―ĄĢ
ĢĻ4ĢĐÔÚÕûļöÔËķŊđýģĖÖÐĢŽRtĄũEFHÉĻđýĩÄÃæŧýĘĮķāÉŲĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÏÂÁÐķþīΚŊĘýÖÐĢŽÍžÏóŌÔÖąÏßx=2ΊķÔģÆÖáĄĒĮŌūđýĩã(0ĢŽ1)ĩÄĘĮ ( )
A.y=(xĢ2)2+1B.y=(x+2)2+1
C.y=(xĢ2)2Ģ3D.y=(x+2)2Ģ3
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠķāÏîĘ―ax5+bx3+3x+cĢŽĩąx=0ĘąĢŽļÃīúĘýĘ―ĩÄÖĩΊĐ1ĢŪ
ĢĻ1ĢĐĮócĩÄÖĩĢŧ
ĢĻ2ĢĐŌŅÖŠĩąx=3ĘąĢŽļÃĘ―ŨÓĩÄÖĩΊ9ĢŽĘÔĮóĩąx=Đ3ĘąļÃĘ―ŨÓĩÄÖĩĢŧ
ĢĻ3ĢĐÔÚĩÚĢĻ2ĢĐÐĄĖâĩÄŌŅÖŠĖõžþÏÂĢŽČôÓÐ3a=5bģÉÁĒĢŽĘÔąČ―Ïa+bÓëcĩÄīóÐĄĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄÏ1=70ĄãĢŽĄÏ2=110ĄãĢŽĄÏC=ĄÏDĢŽĘÔĖ―ËũĄÏAÓëĄÏFÓÐÔõŅųĩÄĘýÁŋđØÏĩĢŽēĒËĩÃũĀíÓÉĢŪ 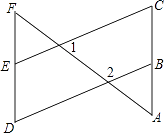
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com