
 已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点
已知:如图,在△AOB中,OB=OA,∠AOB=90°.在△ACQ中,AC=CQ,∠ACQ=90°,点P为BQ的中点分析 (1)欲证明CM=OC,只要证明△AOC≌△QMC即可.
(2)结论:△OCM是等腰直角三角形,只要证明∠OCM=∠ACQ即可.
(3)结论:QM⊥OA,利用“8字型”进行证明.
解答 (1)证明:在△BOP和△QMP中,
$\left\{\begin{array}{l}{OP=PM}\\{∠OPB=∠MPQ}\\{BP=PQ}\end{array}\right.$,
∴△BOP≌△QMP,
∴QM=OB=AO,∠MQP=∠OBP=45°+∠ABQ,
∵∠OAC=∠OAB+∠BAQ+∠QAC=90°+∠BAQ,
∠MQC=360°-∠AQC-∠AQB=∠BQM=360°-45°-(180°-∠QAB-∠ABQ)-(45°+∠ABQ)=90°+∠QAB.
∴∠MQC=∠OAC,
在△AOC和△QMC中,
$\left\{\begin{array}{l}{AO=QM}\\{∠OAC=∠MQC}\\{AC=CQ}\end{array}\right.$,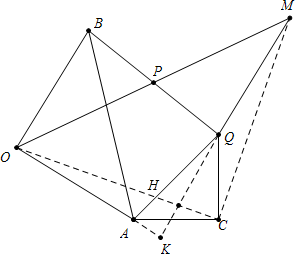
∴△AOC≌△QMC,
∴CM=CO,
(2)结论:△OCM是等腰直角三角形,理由:
证明:∵△AOC≌△QMC,
∴∠ACO=∠QCM,
∴∠OCM=∠ACQ=90°,
∵OC=CM,
∴△OCM是等腰直角三角形.
(3)结论:QM⊥OA,理由:
证明:延长MQ、OA交于点K,OC与KM交于点H,
∵△AOC≌△QMC,
∴∠CMQ=∠COK,
∵∠CMO+∠CHM=90°,∠CHM=∠OHK,
∴∠OHK+∠AOC=90°,
∴∠OKH=90°,
∴QM⊥OA.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质,正确寻找全等三角形是解决问题的关键,学会利用“8字型”证明直角,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
| 甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
| 乙 | 7 | 8 | 9 | 10 | 10 | 10 | 9 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3-x=x(x2-1) | B. | a2-8a+16=(a-4)2 | C. | 5x2+5y2=5(x+y)2 | D. | m2+m-6=(m-3)(m+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.2b}$ | B. | $\sqrt{12a-12b}$ | C. | $\sqrt{x2-y2}$ | D. | $\sqrt{5ab2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com