练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在菱形ABCD中，对角线AC与BD相交于点O，再添加一个条件，仍不能判定四边形ABCD是矩形的是 （　　）

    A.AB＝ADB.OA＝OBC.AC＝BDD.DC⊥BC

    【答案】A

    【解析】

    根据有一个角是直角的平行四边形是矩形，对角线相等的平行四边形是矩形，对各选项分析判断后利用排除法求解．

    A、AB＝AD，则ABCD是菱形，不能判定是矩形，故本选项错误；

    B、OA＝OB，根据平行四边形的对角线互相平分，AC＝BD，对角线相等的平行四边形是矩形可得ABCD是矩形，故本选项正确；

    C、AC＝BD，根据对角线相等的平行四边形是矩形，故本选项正确；

    D、DC⊥BC，则∠BCD＝90°，根据有一个角是直角的平行四边形是矩形可得ABCD是矩形，故本选项正确．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“五一”假期，黔西南州某公司组织部分员工分别到甲、乙、丙、丁四地考察，公司按定额购买了前往各地的车票，如图所示是用来制作完整的车票种类和相应数量的条形统计图，根据统计图回答下列问题：

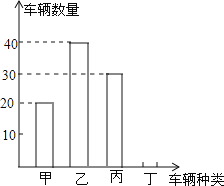
    （1）若去丁地的车票占全部车票的10%，请求出去丁地的车票数量，并补全统计图（如图所示）．

    （2）若公司采用随机抽取的方式发车票，小胡先从所有的车票中随机抽取一张（所有车票的形状、大小、质地完全相同、均匀），那么员工小胡抽到去甲地的车票的概率是多少？

    （3）若有一张车票，小王和小李都想去，决定采取摸球的方式确定，具体规则：“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球（球除数字不同外完全相同），并放回让另一人摸，若小王摸得的数字比小李的小，车票给小王，否则给小李．”试用列表法或画树状图的方法分析这个规则对双方是否公平？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种商品的标价为600元/件，经过两次降价后的价格为486元/件，并且两次降价的百分率相同.

    (1)求该种商品每次降价的百分率；

    (2)若该种商品进价为460元/件，两次降价共售出此种商品100件，为使两次降价销售的总利润不少于3788元.问第一次降价后至少要售出该种商品多少件?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y＝﹣x+4与坐标轴分别交于点A、B，与直线y＝x交于点C．在线段OA上，动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动，同时动点P从点A出发向点O做匀速运动，当点P、Q其中一点停止运动时，另一点也停止运动．分别过点P、Q作x轴的垂线，交直线AB、OC于点E、F，连接EF．若运动时间为t秒，在运动过程中四边形PEFQ总为矩形（点P、Q重合除外）．

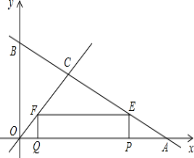
    （1）求点P运动的速度是多少？

    （2）当t为多少秒时，矩形PEFQ为正方形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

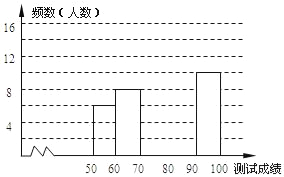
    【题目】 “赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：

    请结合图表完成下列各题：

    （1）①表中a的值为 ，中位数在第 组；

    ②频数分布直方图补充完整；

    （2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？

    （3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．

    组别

    成绩x分

    频数（人数）

    第1组

    50≤x＜60

    6

    第2组

    60≤x＜70

    8

    第3组

    70≤x＜80

    14

    第4组

    80≤x＜90

    a

    第5组

    90≤x＜100

    10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

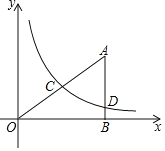
    【题目】如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直于x轴，垂足为点B，反比例函数y＝(x＞0)的图象经过AO的中点C，交AB于点D，且AD＝3．

    (1)设点A的坐标为(4，4)则点C的坐标为　 　；

    (2)若点D的坐标为(4，n)．

    ①求反比例函数y＝的表达式；

    ②求经过C，D两点的直线所对应的函数解析式；

    (3)在(2)的条件下，设点E是线段CD上的动点(不与点C，D重合)，过点E且平行y轴的直线l与反比例函数的图象交于点F，求△OEF面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为更精准地关爱留守学生，某学校将留守学生的各种情形分成四种类型：A．由父母一方照看；B．由爷爷奶奶照看；C．由叔姨等近亲照看；D．直接寄宿学校．某数学小组随机调查了一个班级，发现该班留守学生数量占全班总人数的20%，并将调查结果制成如下两幅不完整的统计图．

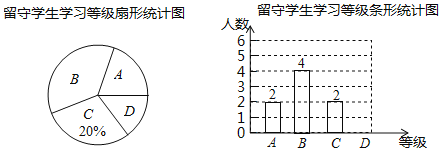
    （1）该班共有　 　名留守学生，B类型留守学生所在扇形的圆心角的度数为　 　；

    （2）将条形统计图补充完整；

    （3）已知该校共有2400名学生，现学校打算对D类型的留守学生进行手拉手关爱活动，请你估计该校将有多少名留守学生在此关爱活动中受益？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：抛物线y＝a（x+1）（x﹣3）与x轴相交于A、B两点，与y轴的交于点C（0，﹣3）．

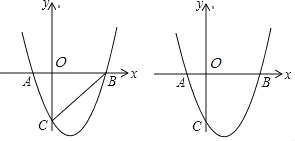
    （1）求抛物线的解析式的一般式．

    （2）若抛物线上有一点P，满足∠ACO＝∠PCB，求P点坐标．

    （3）直线l：y＝kx﹣k+2与抛物线交于E、F两点，当点B到直线l的距离最大时，求△BEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，二次函数（）的图象与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．

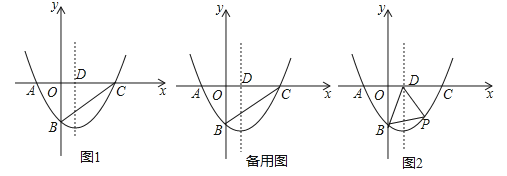
    （1）求该二次函数的解析式；

    （2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；

    （3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．

    查看答案和解析>>

    同步练习册答案