【题目】小明有5张写着不同数的卡片，请你分别按要求抽出卡片，写出符合要求的算式：
(1)从中取出2张卡片，使这2张卡片上的数的乘积最大；
(2)从中取出2张卡片，使这2张卡片上的数相除的商最小；
(3)从中取出2张卡片，使这2张卡片上的数通过有理数的运算后得到的结果最大；
(4)从中取出4张卡片，使这4张卡片通过有理数的运算后得到的结果为24.(写出一种即可)
科目：初中数学 来源： 题型：
【题目】如图，∠B＝∠C，AD∥BC.
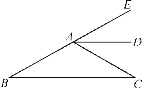
(1)证明：AD平分∠CAE；
(2)如果∠BAC＝120°，求∠B的度数．(不允许使用三角形内角和为180°)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，BC⊥AF于点C，∠A+∠1＝90°．
（1）求证：AB∥DE；
（2）如图2，点P从点A出发，沿线段AF运动到点F停止，连接PB，PE．则∠ABP，∠DEP，∠BPE三个角之间具有怎样的数量关系（不考虑点P与点A，D，C重合的情况）？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图□ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=600，AB=
BC，连接OE ．下列 结论：①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC 成立的个数有（ ）
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
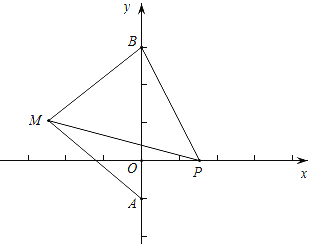
【题目】如图，在平面直角坐标系中，已知A（0，﹣1），B（0，3），点M为第二象限内一点，且点M的坐标为（t，1）．
（1）请用含t的式子表示△ABM的面积；
（2）当t=﹣2时，在x轴的正半轴上有一点P，使得△BMP的面积与△ABM的面积相等，请求出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，ABCD中，E，F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（ ）
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】函数y=
(k＞0)的图象上两点A(x1, y1)和B(x2, y2),且x1＞x2＞0，分别过A、B向x轴作AA1⊥x轴于A1，BB1⊥x轴于B1，则
_________
(填“＞”“=”或“＜”)，若
=2，则函数解析式为_________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某食品加工厂需要一批食品包装盒，供应这种包装盒有两种方案可供选择：
方案一：从包装盒加工厂直接购买，购买所需的费y1与包装盒数x满足如图1所示的函数关系．
方案二：租赁机器自己加工，所需费用y2（包括租赁机器的费用和生产包装盒的费用）与包装盒数x满足如图2所示的函数关系．根据图象回答下列问题：
（1）方案一中每个包装盒的价格是多少元？
（2）方案二中租赁机器的费用是多少元？生产一个包装盒的费用是多少元？
（3）请分别求出y1、y2与x的函数关系式．
（4）如果你是决策者，你认为应该选择哪种方案更省钱？并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
