
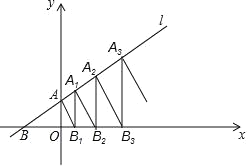
【题目】如图,在平面直角坐标系中,点A,A1,A2,A3…An都在直线1:y=![]() x+1上,点B,B1,B2,B3…Bn都在x轴上,且AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴,则An的横坐标为_________(用含有n的代数式表示)。
x+1上,点B,B1,B2,B3…Bn都在x轴上,且AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴,则An的横坐标为_________(用含有n的代数式表示)。
【答案】![]() ((
((![]() )n﹣1)
)n﹣1)
【解析】
根据题意:先求出AO,A1B1,A2B2的长度,找出规律,表示出AnBn,再计算OBn,可得An的横坐标.
∵直线1:y=![]() x+1交x轴,y轴于B,A两点
x+1交x轴,y轴于B,A两点
∴A(0,1),B(﹣![]() ,0)
,0)
∵AB1⊥1,B1A1⊥x轴,A1B2⊥1,B2A2⊥x轴
∴A1B1∥AO∥A2B2∥A3B3,AB1∥A1B2∥A2B3.
∴∠B=∠OAB1=∠B1A1B2=∠B2A2B3.
∴tan∠B=tan∠OAB1=![]()
∴OB1=![]()
∵OA∥A1B1
∴![]()
∴A1B1=![]()
同理可得A2B2=![]()
…AnBn=(![]() )n
)n
∵OB1=AO×tan∠OAB1=1×![]() =
=![]()
∴B1B2=A1B1×tan∠OAB1=![]() ×
×![]()
…An﹣1Bn=An﹣1Bn﹣1×tan∠OAB1=(![]() )n-1×
)n-1×![]()
∴OBn=OB1+B1B2+B2B3+…+An﹣1Bn﹣1=![]() +
+![]() ×
×![]() +(
+(![]() )2×
)2×![]() +…+(
+…+(![]() )n-1×
)n-1×![]() ①
①
∴![]() OBn=
OBn=![]()
![]()
![]() +(
+(![]() )2×
)2×![]() +…+(
+…+(![]() )n-1×
)n-1×![]() +(
+(![]() )n×
)n×![]() ②
②
∴②﹣①得![]() OBn=(
OBn=(![]() )n ×
)n ×![]() ﹣
﹣![]()
∴OBn=![]() ((
((![]() )n﹣1)
)n﹣1)
故答案为![]() ((
((![]() )n﹣1)
)n﹣1)


科目:初中数学 来源: 题型:
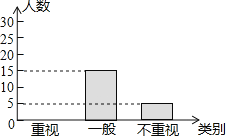
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
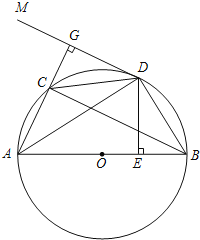
【题目】如图,AB是![]() 的直径,D是
的直径,D是![]() 的中点,
的中点,![]() 于E,交CB于点
于E,交CB于点![]() 过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
![]() 求证:GD是
求证:GD是![]() 的切线;
的切线;
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
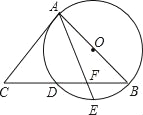
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 2 | 3 | 10 | … |
日销售量(n件) | 198 | 196 | 194 | ? | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格-每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
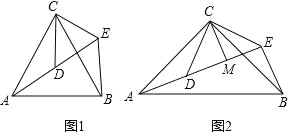
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
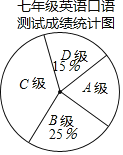
【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为A、B、C、D四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩 | 等级 | 人数 |
| A | 12 |
| B | m |
| C | n |
| D | 9 |
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中C级的圆心角度数;
(3)若该校七年级共有学生640人,根据抽样结课,估计英语口语达到B级以上![]() 包括B级
包括B级![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=8cm,AC=6cm,动点P从点C出发沿CB方向以3cm/s的速度向点B运动,同时动点Q从点B出发沿BA方向以2cm/s的速度向点A运动,将△APQ沿直线AB翻折得△AP′Q,若四边形APQP′为菱形,则运动时间为( )

A. 1sB. ![]()
![]() sC.
sC. ![]() sD.
sD. ![]() s
s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com