
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研其性质——运用函数解决问题”的学习过程.如图,在平面直角坐标系中己经绘制了一条直线![]() .另一函数
.另一函数![]() 与
与![]() 的函数关系如下表:
的函数关系如下表:
| … | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … | -2 | -0.25 | 1 | 1.75 | 2 | 1.75 | 1 | -0.25 | -2 | -4.25 | -7 | -10.25 | -14 | … |
(1)求直线![]() 的解析式;
的解析式;
(2)请根据列表中的数据,绘制出函数![]() 的近似图像;
的近似图像;
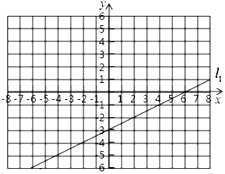
(3)请根据所学知识并结合上述信息拟合出函数![]() 的解折式,并求出
的解折式,并求出![]() 与
与![]() 的交点坐标.
的交点坐标.
科目:初中数学 来源: 题型:
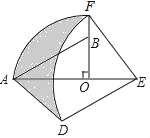
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
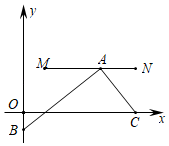
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
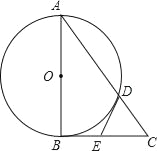
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)求证:4DE2=CDAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学测试中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级 | 平均分 | 中位数 | 方差 |
甲班 |
|
|
|
乙班 |
|
|
|
数学老师让同学们针对统计的结果进行一下评估,学生的评估结果如下:
![]() 这次数学测试成绩中,甲、乙两个班的平均水平相同;
这次数学测试成绩中,甲、乙两个班的平均水平相同;
![]() 甲班学生中数学成绩95分及以上的人数少;
甲班学生中数学成绩95分及以上的人数少;
![]() 乙班学生的数学成绩比较整齐,分化较小.
乙班学生的数学成绩比较整齐,分化较小.
上述评估中,正确的是______![]() 填序号
填序号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
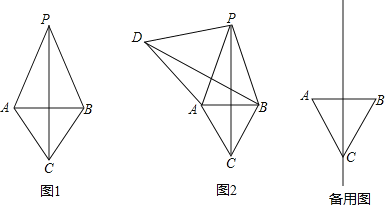
【题目】如图,△ABC是等边三角形,平面上的动点P满足PC⊥AB,记∠APB=α.
(1)如图1,当点P在直线BC上方时,直接写出∠PAC的大小(用含α的代数式表示);
(2)过点B作BC的垂线BD,同时作∠PAD=60°,射线AD与直线BD交于点D.
①如图2,判断△ADP的形状,并给出证明;
②连结CD,若在点P的运动过程中,CD=![]() AB.直接写出此时α的值.
AB.直接写出此时α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班为了配合学校体育文化月活动的开展,同学们从捐助的班费中拿出一部分钱来购买羽毛球拍和跳绳。已知购买一副羽毛球拍比购买一根跳绳多20元。若用200元购买羽毛球拍和用80元购买跳绳,则购买羽毛球拍的副数是购买跳绳根数的一半。
(1)求购买一副羽毛球拍、一根跳绳各需多少元?
(2)双11期间,商店老板给予优惠,购买一副羽毛球拍赠送一根跳绳,如果八(1)班需要的跳绳根数比羽毛球拍的副数的![]() 倍还多
倍还多![]() ,且该班购买羽毛球拍和跳绳的总费用不超过
,且该班购买羽毛球拍和跳绳的总费用不超过![]() 元,那么八(1)班最多可购买多少副羽毛球拍?
元,那么八(1)班最多可购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com