
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.
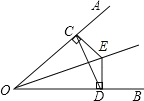
(1)∠ECD和∠EDC相等吗?说明理由.
(2)OC和OD相等吗?说明理由.
(3)OE是线段CD的垂直平分线吗?说明理由.
【答案】(1)、∠ECD=∠EDC,理由见解析;(2)、OC=OD,理由见解析;(3)、OE是线段CD的垂直平分线;理由见解析
【解析】
试题分析:(1)、根据角平分线的性质得出CE=DE,从而得出△CDE为等腰三角形,从而得出答案;(2)、根据角平分线的性质得出Rt△ODE和Rt△OCE全等,从而得出答案;(3)、根据CE=DE,OC=OD得出答案.
试题解析:(1)、∠EDC与∠ECD相等
∵OE是∠AOB的平分线,EC⊥OA,ED⊥OB, ∴EC=ED,∴△CED是等腰三角形, ∴∠EDC=∠ECD;
(2)、OC与OD相等
∵EC⊥OA,ED⊥OB,∴∠ODE=∠OCE=90° 在Rt△ODE和Rt△OCE中,OE=OE(公共边),DE=CE
∴Rt△ODE≌Rt△OCE(HL) ∴OD=OC
(3)、OE是线段CD的垂直平分线
∵EC=ED,∴E点在线段CD的垂直平分线上 ∵OC=OD,∴O点在线段CD的垂直平分线上,
∴OE是线段CD的垂直平分线.


科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
①三角形中最大内角一定不小于600;
② 所有等腰直角三角形都相似;
③正多边形的外角为240,则它的中心角也为240;
④顺次连接对角线相等的四边形各边中点得到矩形.
A. ①② B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店 3 月份、4 月份出售同一品牌各种规格的空调台数如下表;根据表中的数据 回答下列问题:
规格 月份 | A 型号 | B 型号 | C 型号 | D 型号 |
三月 | 12台 | 20台 | 8台 | 4台 |
四月 | 16台 | 30台 | 8台 | 6台 |
(1)商店这两个月平均每月销售空调____台;
(2)请你帮助该商店经理考虑下,6月份进货时,商店对____型号的空调要多进,对_______型号的空调要少进.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上表示整数的点称为整数点,某数轴的单位长度是1㎝,若在这个数轴上随意画出一条长2009㎝的线段AB,被线段AB盖住的整数有( )
A.2006个或2007个
B.2007个或2008个
C.2008个或2009个
D.2009个或2010个
查看答案和解析>>
科目:初中数学 来源: 题型:
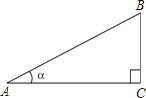
【题目】如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)ctan30°= ;
(2)如图,已知tanA=![]() ,其中∠A为锐角,试求ctanA的值.
,其中∠A为锐角,试求ctanA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com