
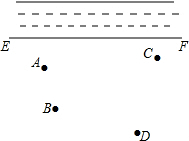
 作图题:如图,在黄河下游一段直线状的河道EF旁边的平原(同一平面)上有A,B,C,D四个小镇,为解决当地供水问题,政府准备投资修建一个蓄水池.
作图题:如图,在黄河下游一段直线状的河道EF旁边的平原(同一平面)上有A,B,C,D四个小镇,为解决当地供水问题,政府准备投资修建一个蓄水池.科目:初中数学 来源: 题型:选择题
| A. | 100m | B. | 150m | C. | 200m | D. | 250m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
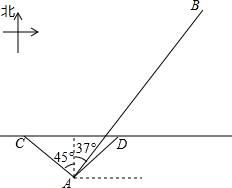 我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.
我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.98×107 | B. | 9.98×108 | C. | O.998×109 | D. | 99.8×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com