
| A. | 100m | B. | 150m | C. | 200m | D. | 250m |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若一个凸四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫做这个四边形的“等腰线”.
若一个凸四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫做这个四边形的“等腰线”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 10 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
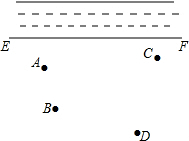 作图题:如图,在黄河下游一段直线状的河道EF旁边的平原(同一平面)上有A,B,C,D四个小镇,为解决当地供水问题,政府准备投资修建一个蓄水池.
作图题:如图,在黄河下游一段直线状的河道EF旁边的平原(同一平面)上有A,B,C,D四个小镇,为解决当地供水问题,政府准备投资修建一个蓄水池.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com