
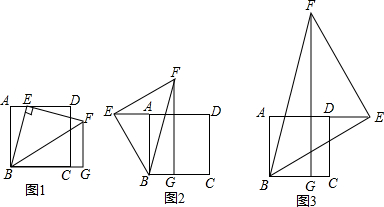
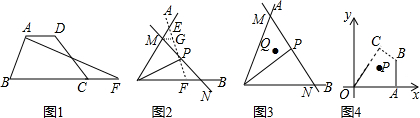
分析 (1)延长AD交GF的延长线于M,根据正方形的性质和全等三角形的判定定理证明△ABE≌△MEF,得到AB=EM,证明结论;
(2)证明△ABE≌△HEF,得到AB=EH,证明结论;
(3)证明△ABE≌△NEF,得到AB=EN,证明结论.
解答 (1)证明:延长AD交GF的延长线于M,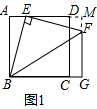
∵四边形ABCD是正方形,
∴∠A=90°,∠ABC=90°,又FG⊥BC,
∴四边形ABGM是矩形,
∴AM=BG,
∵∠A=90°,EF⊥BE,∠M=90°,
∴∠AEB=∠MFE,
在△ABE和△MEF中,
$\left\{\begin{array}{l}{∠A=∠M}\\{∠AEB=∠MFE}\\{EB=EF}\end{array}\right.$,
∴△ABE≌△MEF,
∴AB=EM,
∵AM=AE+EM=AE+AB,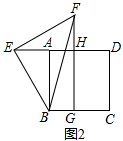
∴AB+AE=BG;
(2)AB-AE=BG.
证明:∵∠FEH+∠BEA=90°,∠BEA+∠ABE=90°,
∴∠FEH=∠ABE,
在△ABE和△HEF中,
$\left\{\begin{array}{l}{∠BAE=∠EHF}\\{∠ABE=∠HEF}\\{EB=EF}\end{array}\right.$,
∴△ABE≌△HEF,
∴EH=AB,
EH-AE═AB-AE=AH,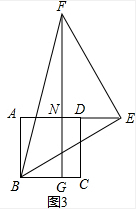
∵四边形ABGH是矩形,
∴AH=BG,
∴AB-AE=BG;
(3)AE=AB+BG.
证明:由(2)得,△ABE≌△NEF,
∴NE=AB,
∵AN+NE=AN+AB=AE,BG=AN,
∴AE=AB+BG.
点评 本题考查的是正方形的性质、矩形的判定和性质、全等三角形的判定和性质,掌握正方形的性质定理、全等三角形的判定定理和性质定理是解题的关键,注意类比思想在解题中的灵活运用.


科目:初中数学 来源: 题型:解答题
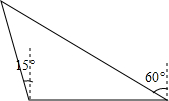 如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有4种拼接方法.
如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有4种拼接方法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 一台电风扇 | 一台收音机 | 谢谢参与 |
| 谢谢参与 | 一副球拍 | 一个U盘 |
| 两张电影票 | 谢谢参与 | 一副球拍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100m | B. | 150m | C. | 200m | D. | 250m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com