
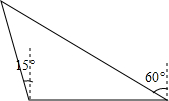
 如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离. 分析 根据题意可以得到∠ABC和∠BCA的度数,从而可以得到∠BAC的度数,作辅助线BD⊥AC,根据题目中的信息可以分别求得AD和CD的长,从而可以得到AC的长.
解答 解:由已知可得,图形如下,
∵∠ABC=90°+15°=105°,∠ACB=90°-60°=30°,
∴∠BAC=180°-∠ABC-∠ACB=180°-105°-30°=45°,
作BD⊥AC于点D,如上图所示,
∵∠BDA=90°,∠A=45°,AB=1000,
∴BD=AD=500$\sqrt{2}$,
又∵∠BDC=90°,∠BCD=30°,BD=500$\sqrt{2}$,
∴CD=$\frac{BD}{tan30°}=\frac{500\sqrt{2}}{\frac{\sqrt{3}}{3}}=500\sqrt{6}$,
∴AC=AD+CD=$500\sqrt{2}+500\sqrt{6}$,
即∠BAC=45°,A,C两学校之间的距离是($500\sqrt{2}+500\sqrt{6}$)米.
点评 本题考查解直角三角形的应用-方向角问题,解题的关键是明确题意,找出所求问题需要的条件,作出合适的辅助线,注意辅助线要用虚线.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 633.6(1+x)2=400(1+10%) | B. | 633.6(1+2x)2=400×(1010%) | ||
| C. | 400×(1+10%)(1+2x)2=633.6 | D. | 400×(1+10%)(1+x)2=633.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
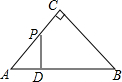 如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A-C-B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A-C-B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )| A. | 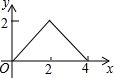 | B. | 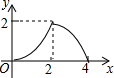 | C. | 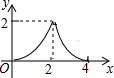 | D. | 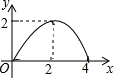 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
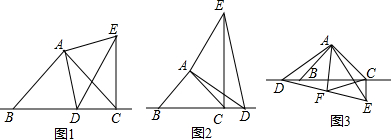
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
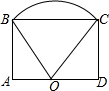 如图,点O是矩形ABCD的边AD的中点,以O为圆心画$\widehat{BC}$,一个动点P从O出发沿线段OA→线段AB→$\widehat{BC}$→线段CD→线段DO作匀速运动,最后回到点O,设OP=y,运动时间为x,则y关于x的函数图象可能是( )
如图,点O是矩形ABCD的边AD的中点,以O为圆心画$\widehat{BC}$,一个动点P从O出发沿线段OA→线段AB→$\widehat{BC}$→线段CD→线段DO作匀速运动,最后回到点O,设OP=y,运动时间为x,则y关于x的函数图象可能是( )| A. | 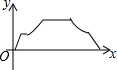 | B. | 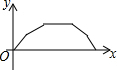 | C. | 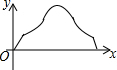 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
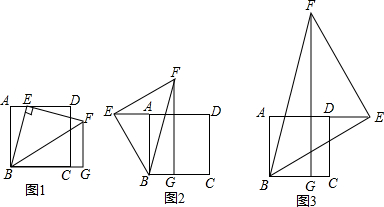
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com