
分析 (1)利用原抛物线上的关于y轴对称的点的特点:纵坐标相同,横坐标互为相反数就可以解答.
(2)设平移后的解析式为:y=(x-h)2,代入点(1,4)求得h的值即可.
解答 解:(1)配方,y=x2-4x+3=(x-2)2-1.
∴抛物线C:顶点(2,-1),与y 轴交点(0,3)
∵C1与C关于y轴对称,
∴C1顶点坐标是(-2,-1),且与y轴交点(0,3).
设C1的解析式为y=a(x+2)2-1、把(0,3)代入,解得:a=1,
∴C1的解析式为y=x2+4x+3.
(2)由题意,可设平移后的解析式为:y=(x-h)2,
∵抛物线C2经过点(1,4),
∴(1-h)2=4,解得:h=-1或h=3,
∴C2的解析式为:y=(x+1)2或y=(x-3)2,
即y=x2+2x+1或y=x2-6x+9.
点评 本题考查了二次函数的图象与几何变换,解决本题的关键是抓住关于y轴对称的坐标特点和平移的规律.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
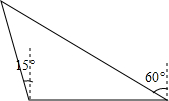 如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 一台电风扇 | 一台收音机 | 谢谢参与 |
| 谢谢参与 | 一副球拍 | 一个U盘 |
| 两张电影票 | 谢谢参与 | 一副球拍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
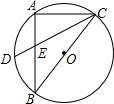 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )| A. | 7:2 | B. | 5:2 | C. | 4:1 | D. | 3:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
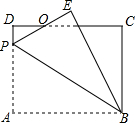 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD=1,则AP的长为3.6.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD=1,则AP的长为3.6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100m | B. | 150m | C. | 200m | D. | 250m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com