
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 一台电风扇 | 一台收音机 | 谢谢参与 |
| 谢谢参与 | 一副球拍 | 一个U盘 |
| 两张电影票 | 谢谢参与 | 一副球拍 |
分析 (1)由共有9种等可能的结果,只有1种情况是一台电风扇,直接利用概率公式求解即可求得答案;
(2)由题意可得共有等可能的结果:9×9=81(种),其中都是“谢谢参与”的有9种情况,则可求得答案.
解答 解:(1)∵共有9种等可能的结果,只有1种情况是一台电风扇,
∴一张抽奖券翻到一台电风扇的概率为:$\frac{1}{9}$;
(2)∵共有等可能的结果:9×9=81(种),其中都是“谢谢参与”的有9种情况,
∴两张抽奖券都是“谢谢参与”的概率为:$\frac{1}{9}$.
事件:得到总是“谢谢参与”的概率.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
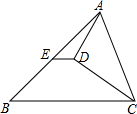 如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某地4月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )
某地4月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )| A. | 19,19 | B. | 19,19.5 | C. | 21,22 | D. | 20,20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
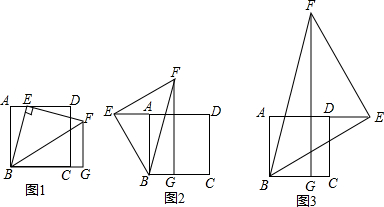
 若一个凸四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫做这个四边形的“等腰线”.
若一个凸四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫做这个四边形的“等腰线”.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com