
| ���� | һ | �� | �� | �� | �� | �� | �� |
| ������ֵ | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
���� ��1�����ݼ�¼��֪��С�������������������30-4=26����
��2���Ȱ�������������ӣ�Ȼ������������ļӷ����㷨����м��㣬�ټ��ϼƻ����������ɣ�
��3���ȼ���ÿ��Ĺ��ʣ�����Ӽ�����⣻
��4���ȼ��㳬����ɼ�����ߣ�Ȼ�������㹤�ʣ�
��� �⣺��1��30-4=26��
�ʴ�Ϊ��26��
��2����+10��+��-12��+��-4��+��+8��+��-1��+��+6��+0
=10-12-4+8-1+6
=7��
��210+7=217��������
�ʱ���ʵ���������217����
�ʴ�Ϊ��217��
��3��217��5+��10+8+6����3+��12+4+1������-2��
=1123��Ԫ����
��С��������һ�ܵĹ����ܶ���1123Ԫ��
��4��ÿ�ܼƼ�һ�ܵ�1106Ԫ��
��Ϊ1123��1106������ÿ�ռƼ����ʸ��࣮
���� ���⿼���������븺�����������Ӽ�������㣬�����������ݣ���������ȷ��ʽ�ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 3n�� | B�� | ��3n+1���� | C�� | ��3n+2���� | D�� | ��3n+3���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��12 | B�� | 2��-12 | C�� | 2��12 | D�� | -2��-12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
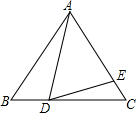 ��ͼ���ڱ߳�Ϊ18����������ABC�У�BD=6����ADE=60�㣬��AE�ij�Ϊ14��
��ͼ���ڱ߳�Ϊ18����������ABC�У�BD=6����ADE=60�㣬��AE�ij�Ϊ14���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+b��0 | B�� | a-b��0 | C�� | a•b��0 | D�� | ��-$\frac{b}{a}$��3��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
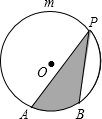 ��ͼ��AB��Բ�ڽ��������ε�һ�ߣ��������εİ뾶Ϊ2����P�ڻ�AmB�ϣ���P��ֱ��AB�ľ���Ϊ3����ͼ����Ӱ���ֵ����Ϊ��������
��ͼ��AB��Բ�ڽ��������ε�һ�ߣ��������εİ뾶Ϊ2����P�ڻ�AmB�ϣ���P��ֱ��AB�ľ���Ϊ3����ͼ����Ӱ���ֵ����Ϊ��������| A�� | 3 | B�� | $\frac{2��}{3}$ | C�� | $\frac{2��}{3}$+3 | D�� | $\frac{2��}{3}$-$\sqrt{3}$+3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com