
【题目】如图,一枚棋子放在⊙O上的点A处,通过摸球来确定该棋子的走法.
其规则如下:在一只不透明的口袋中,装有3个标号分别为1,2,3的相同小球.充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,若摸出的两个小球标号之积是m,就沿着圆周按逆时针方向走m步(例如:m=1,则A﹣B;若m=6,则A﹣B﹣C﹣D﹣A﹣B﹣C).用列表或树状图,分别求出棋子走到A、B、C、D点的概率.
【答案】解:画树状图得:
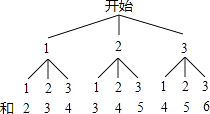
∵共有9种等可能的结果,棋子走到A点的有3种情况(点数和为4),棋子走到B点的有2种情况(点数和为5),棋子走到C点的有2种情况(点数和为2或6),棋子走到D点的有2种情况(点数和为3),
∴P(棋子走到A点)= ![]() =
= ![]() ,P(棋子走到B点)=P(棋子走到C点)=P(棋子走到D点)=
,P(棋子走到B点)=P(棋子走到C点)=P(棋子走到D点)= ![]() .
.
【解析】抓住题中关键的已知条件,充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,画出树状图,求出所有可能的结果数,及分别求出棋子走到A点、棋子走到B点、棋子走到C点、棋子走到D的可能数,然后利用概率公式即可求出它们的概率。
【考点精析】本题主要考查了列表法与树状图法的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】请在横线上和括号内填上推导内容或依据.
如图,已知 ![]() ,
, ![]() ,求证:
,求证: ![]() .
.

证明: ![]() (已知),
(已知),
![]() ( ),
( ),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
∵![]() (已知),
(已知),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
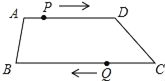
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点
两点
(1)求![]() 点的坐标,并在网格中用两点法画出直线
点的坐标,并在网格中用两点法画出直线![]() ;
;
(2)将直线![]() 向上平移6个单位后得到直线
向上平移6个单位后得到直线![]() ,画出平移后的直线
,画出平移后的直线![]() ,并直接写出直线
,并直接写出直线![]() 的函数解析式
的函数解析式
(3)设直线![]() 与
与![]() 轴交于点M,求
轴交于点M,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校兴趣小组,对函数y=|x﹣1|+1的图像和性质进行了研究,探究过程如下:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值如表:
的几组对应值如表:
X | …… |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | …… |
y | …… | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | …… |
其中![]()
(2)在平面直角坐标系中,画出上表中对应值为点的坐标,根据画出的点,画出该函数的图象;

(3)根据画出的函数图像特征,仿照示例,完成下表中函数的变化规律:
序号 | 函数图像特征 | 函数变化规律 |
示例1 | 在直线 | 当 |
① | 在直线 |
|
示例2 | 函数图像经过点(-3,5) | 当 |
② | 函数图像的最低点是 | 当 |
(4)当![]() 时,
时,![]() 的取值范围是_____________
的取值范围是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.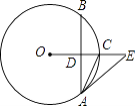
(1)求证:直线AE是⊙O的切线;
(2)若AB=8,sin∠E= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是( )
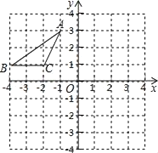
A.A1(4,4),C1(3,2)B.A1(3,3),C1(2,1)
C.A1(4,3),C1(2,3)D.A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 . (写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
(1)求证:∠ADC=∠ABD;
(2)若AD=2 ![]() ,⊙O的半径为3,求MD的长.
,⊙O的半径为3,求MD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com