
【题目】已知直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点
两点
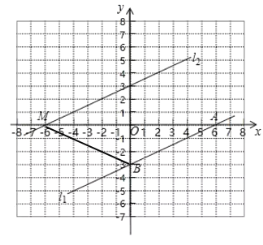
(1)求![]() 点的坐标,并在网格中用两点法画出直线
点的坐标,并在网格中用两点法画出直线![]() ;
;
(2)将直线![]() 向上平移6个单位后得到直线
向上平移6个单位后得到直线![]() ,画出平移后的直线
,画出平移后的直线![]() ,并直接写出直线
,并直接写出直线![]() 的函数解析式
的函数解析式
(3)设直线![]() 与
与![]() 轴交于点M,求
轴交于点M,求![]() 的面积.
的面积.

【答案】(1)(6, 0),(0,-3),见解析;(2)见解析,![]() ;(3)18
;(3)18
【解析】
(1)根据自变量与函数值的对应关系,即可得到答案;
(2)根据图象平移的规律:左加右减,上加下减,即可得到图象和解析式;
(3)把![]() 代入
代入![]() 求得M的坐标是(-6, 0),由点A、点B的坐标得到AM=12,BO=3,再根据三角形面积公式即可得到答案.
求得M的坐标是(-6, 0),由点A、点B的坐标得到AM=12,BO=3,再根据三角形面积公式即可得到答案.
解:(1)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴点A的坐标是(6, 0),点B的坐标是(0,-3).
直线![]() 如图所示
如图所示
(2)直线![]() 如图所示,直线
如图所示,直线![]() 的解析式为
的解析式为![]()
(3)把![]() 代入
代入![]() 得,
得,![]() ,解得
,解得![]() .
.
∴点M的坐标是(-6, 0),
∵点A的坐标是(6, 0),点B的坐标是(0,-3)
∴AM=6-(-6)=12,BO=3
∴S△MAB=![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图E是平行四边形![]() 边BC上一点,且
边BC上一点,且![]() ,连接AE,并延长AE与DC的延长线交于点F,
,连接AE,并延长AE与DC的延长线交于点F, ![]() .
.
(1)请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求![]() 的各内角的大小.
的各内角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚棋子放在⊙O上的点A处,通过摸球来确定该棋子的走法.
其规则如下:在一只不透明的口袋中,装有3个标号分别为1,2,3的相同小球.充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,若摸出的两个小球标号之积是m,就沿着圆周按逆时针方向走m步(例如:m=1,则A﹣B;若m=6,则A﹣B﹣C﹣D﹣A﹣B﹣C).用列表或树状图,分别求出棋子走到A、B、C、D点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架方梯AB长25米,如图所示,斜靠在一面上:

(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com