
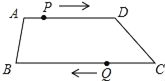
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
【答案】(1)t,12﹣t,15﹣2t,2t(2)t=5s时四边形APQB是平行四边形(3)当t=4s时,四边形PDCQ是平行四边形
【解析】
(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长;
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
解:(1)AP=t,DP =12﹣t,BQ=15﹣2t,CQ=2t;
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形,
∴t=15﹣2t,解得t=5,
∴t=5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1,∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚棋子放在⊙O上的点A处,通过摸球来确定该棋子的走法.
其规则如下:在一只不透明的口袋中,装有3个标号分别为1,2,3的相同小球.充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,若摸出的两个小球标号之积是m,就沿着圆周按逆时针方向走m步(例如:m=1,则A﹣B;若m=6,则A﹣B﹣C﹣D﹣A﹣B﹣C).用列表或树状图,分别求出棋子走到A、B、C、D点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于 ![]() 的一元二次方程
的一元二次方程 ![]() 的两个根,且OA>OB
的两个根,且OA>OB
(1)求cos∠ABC的值。
(2)若E为x轴上的点,且 ![]() ,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com