
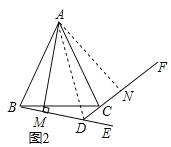
【题目】如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
(1)探究∠BDC和∠CAB的数量关系并说明理由;
(2)求证:BM=DM+DC;
(3)如图2,将射线BE,CF分别绕点B和点C顺时针旋转至如图位置,若∠ABE=∠ACF仍然成立,射线BE交射线CF的反向延长线于点D,过A点作AM⊥BD于M.请问(2)中的结论是否还成立?如果成立,请证明.如果不成立,线段BM,DM,DC又有怎样的数量关系?并证明你的结论.
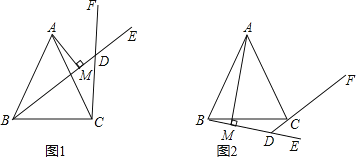
【答案】(1)∠BDC=∠CAB,见解析;(2)见解析;(3)不成立,BM=DM﹣DC,见解析
【解析】
(1)由三角形内角和定理得出![]() ,
,![]() ,又∠ABE=∠ACF,则进行计算即可得解;
,又∠ABE=∠ACF,则进行计算即可得解;
(2)作AN⊥CF于N,连接AD,易证![]() ,由AAS证得△AMB≌△ANC得出BM=CN=DC+DN,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论;
,由AAS证得△AMB≌△ANC得出BM=CN=DC+DN,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论;
(3)作AN⊥CF于N,连接AD,易证![]() ,由AAS证得△AMB≌△ANC得出
,由AAS证得△AMB≌△ANC得出![]() ,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论.
,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论.
(1)解:∠BDC=∠CAB;理由如下:
∵![]() ,
,
![]() ,
,
∠ABE=∠ACF,
∴![]()
=![]()
=![]()
∴![]() ;
;
(2)证明:作AN⊥CF于N,连接AD,如图1所示:
∵AM⊥BD,
∴![]() ,
,
在△AMB和△ANC中,
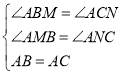 ,
,
∴△AMB≌△ANC![]() ,
,
∴BM=CN=DC+DN,AM=AN,
在Rt△AMD和Rt△AND中,
![]() ,
,
∴Rt△AMD≌Rt△AND![]() ,
,
∴DM=DN,
∴BM=DM+DC;
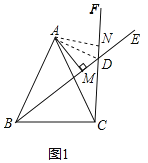
(3)不成立,BM=DM﹣DC;理由如下:
作AN⊥CF于N,连接AD,如图2所示:
∵AM⊥BD,
∴![]() ,
,
在△AMB和△ANC中,
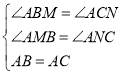 ,
,
∴△AMB≌△ANC![]() ,
,
∴![]() ,AM=AN,
,AM=AN,
在Rt△AMD与Rt△AND中,
![]() ,
,
∴Rt△AMD≌Rt△AND![]() ,
,
∴DM=DN,
∴![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
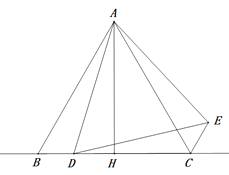
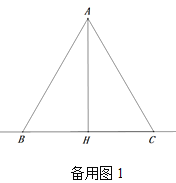
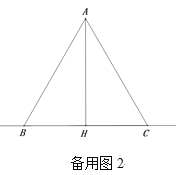
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:∠ABC=∠ACB;
(2)当D在线段BC上时,
①求证:△BAD≌△CAE;②当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
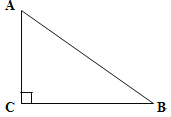
【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
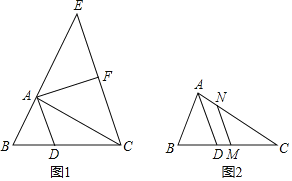
【题目】在△ABC中,AD是△ABC的角平分线.
(1)如图1,过C作CE∥AD交BA延长线于点E,若F为CE的中点,连接AF,求证:AF⊥AD.
(2)如图1,在(1)的条件下,若CD=2BD,S△ABD=10,求△BCE的面积.
(3)如图2,M为BC的中点,过M作MN∥AD交AC于点N,猜想线段AB、AC、AN之间的数量关系?请写出你的猜想,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游公司大巴从旅行社出发,先向西行驶3千米到达![]() 景点,再继续向西行驶2千米到达
景点,再继续向西行驶2千米到达![]() 景点,然后向东行驶7千米到达
景点,然后向东行驶7千米到达![]() 景点,最后回到旅行社.
景点,最后回到旅行社.
(1)以旅行社为原点,以向东方向为正方向,用1个单位长度表示1千米,画出数轴,并在该数轴上表示出![]() 、
、![]() 、
、![]() 三个景点的位置.
三个景点的位置.
(2)![]() 景点距离
景点距离![]() 景点多远?
景点多远?
(3)该旅游大巴共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
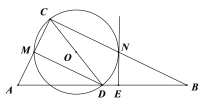
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,解答后面的问题:“十字相乘法”能将二次三项式分解因式,对于形如![]() 的关于
的关于![]() ,
,![]() 的二次三项式来说,方法的关键是将
的二次三项式来说,方法的关键是将![]() 项系数
项系数![]() 分解成两个因数
分解成两个因数![]() ,
,![]() 的积,即
的积,即![]() ,将
,将![]() 项系数
项系数![]() 分解成两个因式
分解成两个因式![]() ,
,![]() 的积,即
的积,即![]() ,并使
,并使![]() 正好等于
正好等于![]() 项的系数
项的系数![]() ,那么可以直接写成结果:
,那么可以直接写成结果:![]()
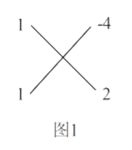
例:分解因式:![]()
解:如图1,其中![]() ,
,![]() ,而
,而![]()
所以![]()
而对于形如![]() 的关于
的关于![]() ,
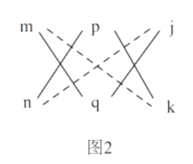
,![]() 的二元二次式也可以用十字相乘法来分解.如图2.将
的二元二次式也可以用十字相乘法来分解.如图2.将![]() 分解成
分解成![]() 乘积作为一列,
乘积作为一列,![]() 分解成
分解成![]() 乘积作为第二列,
乘积作为第二列,![]() 分解成
分解成![]() 乘积作为第三列,如果
乘积作为第三列,如果![]() ,
,![]() ,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式
,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式![]()
例:分解因式![]()
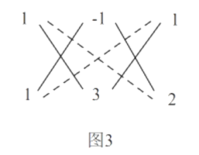
解:如图3,其中![]() ,
,![]() ,
,![]()
而![]() ,
,![]() ,
,![]()
所以![]()
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:①![]() .
.
②![]() .
.
(2)若关于![]() ,
,![]() 的二元二次式
的二元二次式![]() 可以分解成两个一次因式的积,求
可以分解成两个一次因式的积,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com