
【题目】在△ABC中,AD是△ABC的角平分线.
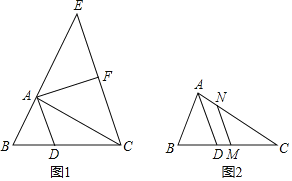
(1)如图1,过C作CE∥AD交BA延长线于点E,若F为CE的中点,连接AF,求证:AF⊥AD.
(2)如图1,在(1)的条件下,若CD=2BD,S△ABD=10,求△BCE的面积.
(3)如图2,M为BC的中点,过M作MN∥AD交AC于点N,猜想线段AB、AC、AN之间的数量关系?请写出你的猜想,并给予证明.
【答案】(1)见解析;(2)90;(3)AC=AB+2AN,见解析
【解析】
(1)角平分线的定义得出∠BAD=∠CAD,由平行线的性质得出∠BAD=∠E,∠CAD=∠ACE,则∠E=∠ACE,由等腰三角形的性质得出AC=AE,AF⊥EC,推出![]() ,即可得出结论;
,即可得出结论;
(2)求出BC=3BD,证出△ABD∽△EBC,则![]()
![]() ,即可得出结果;
,即可得出结果;
(3)延长BA与MN延长线于点E,过B作BF∥AC交NM延长线于点F,则∠MBF=∠C,∠F=∠MNC,由中点得出BM=CM,由AAS证得△BFM≌△CNM得出BF=CN,由MN∥AD,得出∠BAD=∠E,∠CAD=∠MNC=∠ANE,则∠E=∠ANE=∠F,得出AE=AN,BE=BF,推出BF=AB+AN,即可得出结论.
(1)证明:∵AD为△ABC的角平分线,
∴∠BAD=∠CAD,
∵CE∥AD,
∴∠BAD=∠E,∠CAD=∠ACE,
∴∠E=∠ACE,
∴AC=AE,
∵F为EC的中点,
∴AF⊥EC,
∵AD∥EC,
∴![]() ,
,
∴AF⊥AD;
(2)解:∵CD=2BD,
∴BC=3BD,
∴AD∥CE,
∴△ABD∽△EBC,
∴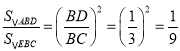 ,
,
∴![]() ;
;
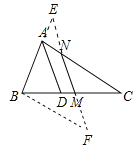
(3)解:AC=AB+2AN;理由如下:
延长BA与MN延长线于点E,过B作BF∥AC交NM延长线于点F,如图2所示:
∴∠MBF=∠C,∠F=∠MNC,
∵M为BC的中点,
∴BM=CM,
在△BFM和△CNM中,
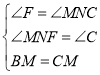 ,
,
∴△BFM≌△CNM(AAS),
∴BF=CN,
∵MN∥AD,
∴![]() ,∠CAD=∠MNC=∠ANE,
,∠CAD=∠MNC=∠ANE,
∴∠E=∠ANE=∠F,
∴AE=AN,BE=BF,
∴BF=AB+AN,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图
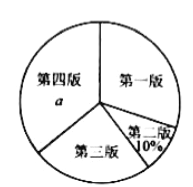

请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,![]()
![]() ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为 ![]() ;
;
(2)请你补全条形统计图;
(3)若该校有![]() 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了解政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1、图2.

小明发现每月每户的用水量为5 ![]() -35
-35 ![]() 之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)![]() ,小明调查了 户居民,并补全图1;
,小明调查了 户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC=90![]() ,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
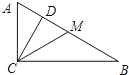
A. ∠ACD=∠BB. CM=![]() C. ∠B=30
C. ∠B=30![]() D. CD=
D. CD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
(1)探究∠BDC和∠CAB的数量关系并说明理由;
(2)求证:BM=DM+DC;
(3)如图2,将射线BE,CF分别绕点B和点C顺时针旋转至如图位置,若∠ABE=∠ACF仍然成立,射线BE交射线CF的反向延长线于点D,过A点作AM⊥BD于M.请问(2)中的结论是否还成立?如果成立,请证明.如果不成立,线段BM,DM,DC又有怎样的数量关系?并证明你的结论.
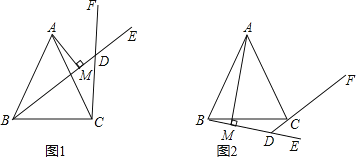
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥CD,∠A=90![]() ,AB=
,AB=![]() ,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
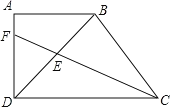
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
x | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | ||
y |
|
|
|
|
| 0 |
|
| m |
|
|
(1)求m的值为 ;
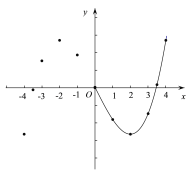
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程![]() 实数根的个数为 ;
实数根的个数为 ;
(4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线![]() ,根据图象写出方程
,根据图象写出方程![]() 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com