练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图在Rt△ABC=90，如果CD、CM分别是斜边上的高和中线，AC=2，BC=4，那么下列结论中错误的是（ ）

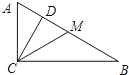
    A. ∠ACD=∠BB. CM=C. ∠B=30D. CD=

    【答案】C

    【解析】

    根据同角的余角相等判断A；根据勾股定理和直角三角形的性质判断B；根据三角形的面积公式计算，判断D．

    ∵∠ACB=90°，∴∠ACD+∠BCD=90°．

    ∵CD⊥AB，∴∠B+∠BCD=90°，∴∠ACD=∠B，故A正确，不符合题意；

    在Rt△ACB中，AB2．

    ∵∠ACB=90°，CM是斜边上的中线，∴CM，故B正确，不符合题意；

    在Rt△ACB中，AB=2，AC=2，∴∠B≠30°，故C错误，符合题意；

    2×42CD，解得：CD，故D正确，不符合题意．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，A（5，0），B（0，5）.

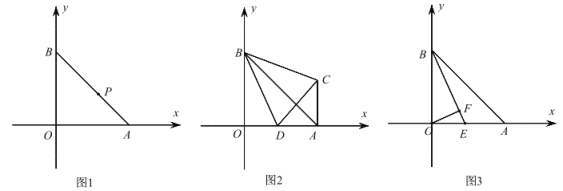
    （1）如图 1，P 是 AB 上一点且，求 P 点坐标；

    （2）如图 2，D 为 OA 上一点，AC∥OB 且∠CBO＝∠DCB，求∠CBD 的度数；

    （3）如图 3，E 为 OA 上一点，OF⊥BE 于 F，若∠BEO＝45°＋∠EOF，求的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为等边三角形，D为边BA延长线上一点，连接CD，以CD为一边作等边三角形CDE，连接AE．

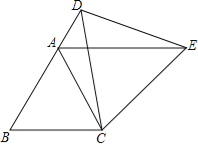
    （1）求证：△CBD≌△CAE．

    （2）判断AE与BC的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为_____．

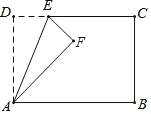
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AC＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，则AE的长为

    A. B. 2 C. D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

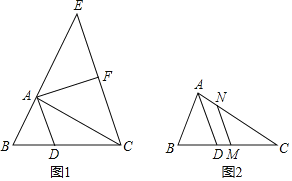
    【题目】在△ABC中，AD是△ABC的角平分线．

    （1）如图1，过C作CE∥AD交BA延长线于点E，若F为CE的中点，连接AF，求证：AF⊥AD．

    （2）如图1，在（1）的条件下，若CD＝2BD，S△ABD＝10，求△BCE的面积．

    （3）如图2，M为BC的中点，过M作MN∥AD交AC于点N，猜想线段AB、AC、AN之间的数量关系？请写出你的猜想，并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义一种新运算“♀”，观察下列运算：

    （+5）♀（+14）=+19，

    ♀=+20,

    ,

    ，

    ，

    (+13)♀0=+13．

    （1）请你认真思考上述运算，归纳运算“♀”的法则．

    两数进行运算“♀”时，同号______，异号_________，特别地，0和任何数进行运算“♀”，或任何数和0进行运算“♀”，结果都为_______．

    （2）计算：♀[0♀]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足＋|b－6|＝0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O－C－B－A－O的线路移动．

    （1）a＝______________，b＝_____________，点B的坐标为_______________；

    （2）当点P移动4秒时，请指出点P的位置，并求出点P的坐标；

    （3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AC=BC，∠ACB=120°，点D在AB边上运动（D不与A、B重合），连结CD．作∠CDE=30°，DE交AC于点E．

    （1）当DE∥BC时，△ACD的形状按角分类是直角三角形；

    （2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由．

    查看答案和解析>>

    同步练习册答案