
【题目】在四边形ABCD中,AB∥CD,∠A=90![]() ,AB=
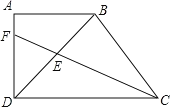
,AB=![]() ,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
【答案】![]() .
.
【解析】
先过点E作EG⊥CD于G,再判定△BCD.△ABD都是等腰直角三角形,并求得其边长,最后利用角平分线的性质和等腰直角三角形的性质,求得EG的长,进而得到△EDC的面积.
过点E作EG⊥CD于G.
又∵CF平分∠BCD,BD⊥BC,∴BE=GE,BC=GC.
∵BD⊥BC,BD=BC,∴△BCD是等腰直角三角形,∴∠BDC=45°.
∵AB∥CD,∴∠ABD=45°.
又∵∠A=90°,AB=![]() ,∴等腰直角三角形ABD中,BD
,∴等腰直角三角形ABD中,BD![]() ,∴BC=2,∴Rt△BDC中,CD
,∴BC=2,∴Rt△BDC中,CD![]() ,∴DG=DC﹣GC=
,∴DG=DC﹣GC=![]() .
.
∵△DEG是等腰直角三角形,∴EG=DG=![]() ,∴△EDC的面积
,∴△EDC的面积![]() DC×EG
DC×EG![]()
![]() ×(
×(![]() )=
)=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
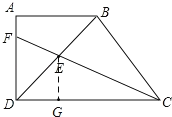
【题目】如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
(1)求点A、B的坐标;
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图 2,求∠AMD的度数;
(3)如图 3,(也可以利用图 1)①求点F的坐标;②坐标轴上是否存在点P,使得△ABP和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
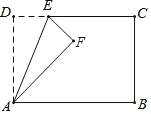
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
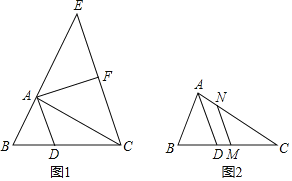
【题目】在△ABC中,AD是△ABC的角平分线.
(1)如图1,过C作CE∥AD交BA延长线于点E,若F为CE的中点,连接AF,求证:AF⊥AD.
(2)如图1,在(1)的条件下,若CD=2BD,S△ABD=10,求△BCE的面积.
(3)如图2,M为BC的中点,过M作MN∥AD交AC于点N,猜想线段AB、AC、AN之间的数量关系?请写出你的猜想,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“♀”,观察下列运算:
(+5)♀(+14)=+19,
![]() ♀
♀![]() =+20,
=+20,
![]() ,
,
![]() ,
,
![]() ,
,
(+13)♀0=+13.
(1)请你认真思考上述运算,归纳运算“♀”的法则.
两数进行运算“♀”时,同号______,异号_________,特别地,0和任何数进行运算“♀”,或任何数和0进行运算“♀”,结果都为_______.
(2)计算:![]() ♀[0♀
♀[0♀![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
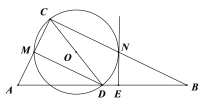
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“节能环保”是对美好家园的一种守护,某汽车制造厂生产一种新型能源汽车,计划半年后每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实际每月生产量与计划量相比情况如下表(增加为正,减少为负):
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
增减(辆) | +3 | -2 | -1 | +4 | +2 | -5 |
(1)生产量最多的一个月,比生产量最少的一个月多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了?多或少多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
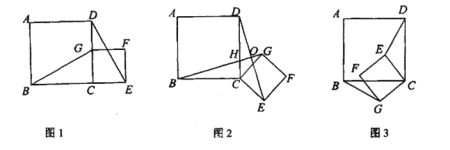
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.(正方形四条边都相等,四个角都是直角)
1.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)猜想图1中线段BG和线段DE的长度和位置关系:______________.
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2.如图3情形.请你通过观察、测量等方法判断上述猜想是否仍然成立:_______(成立、不成立)若成立,请你选取图2或图3中的一种情况说明你的判断.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com