
【题目】如图,长方形OABC的边OC、OA分别在x轴、y轴上,点B的坐标为(![]() ,1)点D是AB边上一个动点(与点A不重合),沿OD将△OAD对折后,点A落到点P处,并满足△PCB是等腰三角形,则P点坐标为____.
,1)点D是AB边上一个动点(与点A不重合),沿OD将△OAD对折后,点A落到点P处,并满足△PCB是等腰三角形,则P点坐标为____.

【答案】(![]() )或(
)或(![]() ).
).
【解析】
连接PB,PC.分三种情况:①若PB=PC,设P(x,![]() ),过P作PH⊥x轴于H.在Rt△OPH中根据勾股定理解得x,从而确定P点坐标;②若BP=BC,则BP=1,连接OB.在Rt△OBC中根据勾股定理求出OB,从而得出P为线段OB中点,求出P点坐标;③若CP=CB,则CP=1,PO=PC,P在OC中垂线上.设P(
),过P作PH⊥x轴于H.在Rt△OPH中根据勾股定理解得x,从而确定P点坐标;②若BP=BC,则BP=1,连接OB.在Rt△OBC中根据勾股定理求出OB,从而得出P为线段OB中点,求出P点坐标;③若CP=CB,则CP=1,PO=PC,P在OC中垂线上.设P(![]() ,y),过P作PH⊥x轴于H,在Rt△OPH中根据勾股定理求出P点坐标即可.
,y),过P作PH⊥x轴于H,在Rt△OPH中根据勾股定理求出P点坐标即可.
连接PB,PC,
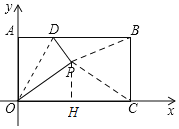
①若PB=PC,则P在BC的中垂线y=![]() 上,
上,
∴设P(x,![]() ),
),
如图,过P作PH⊥x轴于H,
在Rt△OPH中,PH=![]() ,OH=x,OP=1,
,OH=x,OP=1,
∴x2+![]() =1,
=1,
解得:x1=![]() ,x2=-
,x2=-![]() (不合题意),
(不合题意),
∴P(![]() ,
,![]() );
);
②若BP=BC,则BP=1,连接OB,
∵OP=1,
∴OP+PB=2,
∵在Rt△OBC中,∠OCB=90°,OB=![]() =2,
=2,
∴OP+PB=OB,
∴O,P,B三点共线,P为线段OB中点.
又∵B(![]() ,1),
,1),
∴P(![]() ,
,![]() );
);
③若CP=CB,则CP=1,
∵OP=1,
∴PO=PC,则P在OC的中垂线x=![]() 上,
上,
∴设P(![]() ,y).
,y).
过P作PH⊥x轴于H,在Rt△OPH中,PH=|y|,OH=![]() ,OP=1,
,OP=1,
∴y2+![]() =1,
=1,
解得:y1=![]() ,y2=-
,y2=-![]() ,
,
∴P(![]() )或(
)或(![]() ),
),
当点P(![]() )时,∠AOP=120°,此时∠AOD=60°,点D与点B重合,符合题意.
)时,∠AOP=120°,此时∠AOD=60°,点D与点B重合,符合题意.
故答案为:(![]() )或(
)或(![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示.
(1)写出三角形③的顶点坐标.
(2)通过平移由三角形③能得到三角形④吗?
(3)根据对称性由三角形③可得三角形①,②,它们的顶点坐标各是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠EB.BC=EC,AC=DC
C.BC=DC,∠A=∠DD.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 是
是![]() 边上的两个动点,其中点
边上的两个动点,其中点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,且速度为每秒
方向运动,且速度为每秒![]() ,它们同时出发,设出发的时间为
,它们同时出发,设出发的时间为![]() .
.

(1)出发![]() 后,求
后,求![]() 的长;
的长;
(2)当点![]() 在边
在边![]() 上运动时,出发多久后,
上运动时,出发多久后,![]() 能形成等腰三角形?
能形成等腰三角形?
(3)当点![]() 在边
在边![]() 上运动时,求能使
上运动时,求能使![]() 成为等腰三角形的运动时间.
成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ACB中,∠CAB的平分线与过BC边垂直平分线DE交于E点,EF⊥AB,垂足是F,EG⊥AC,垂足是G.

(1)求证:BF=CG;
(2)若AB=a,AC=b(a>b),求BF长(用a、b表示BF长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,为了躲避海盗,一轮船一直由西向东航行,早上8点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,10点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船是否能一直向东航行?

查看答案和解析>>
科目:初中数学 来源: 题型:
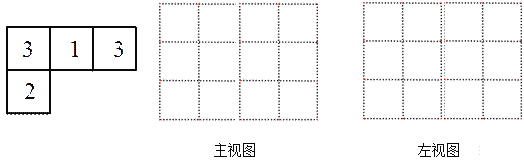
【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com