
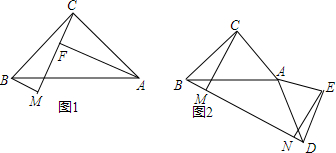
分析 (1)根据全等三角形的判定定理AAS推知△ACF≌△CBM,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换,即可解答;
(2)如图2,过点A作AG⊥CM于G,反向延长GA交EN于H,由四边形GMNH为矩形,得到AH⊥EN,然后易得:△CMB≌△AGC,△AEH≌△EDN,利用全等三角形的对应边相等得到相等的线段,即可解答.
(3)取AB的中点M、AD的中点N,连接PM、CM、NE、PN,则可构造△PNE≌CMP,结论不言而喻.
解答 解:(1)AF=BM+MF,
∵∠ACB=90°,
∴∠ACF+∠BCM=90°.
又∵AF⊥CM,
∴∠ACF+∠CAF=90°,
∴∠CAF=∠BCM.
在△ACF和△CBM中,
$\left\{\begin{array}{l}{∠BMC=∠CFA=9{0}^{°}}\\{∠CAF=∠BCM}\\{AC=CB}\end{array}\right.$,
∴△ACF≌△CBM,
∴BM=CF,AF=CM,
∴CF+MF=BM+MF=MC=AF,即AF=BM+MF.
故答案为:AF=BM+MF.
(2)如图2,过点A作AG⊥CM于G,反向延长GA交EN于H,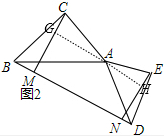
∴四边形GMNH为矩形
∴AH⊥EN
根据三垂直得:△CMB≌△AGC,△AEH≌△EDN,
∴CM=AG,EN=AH,
∴MN=GH=GA+AH=CM+EN.
(3)如图3,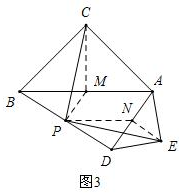
取AB的中点M、AD的中点N,连接PM、CM、NE、PN,
∵△BCA与△AED均为等腰直角三角形,
∴CM=BM=AM,CM⊥BA,
EN=AN=DN,NE⊥AD,
∵P为BD中点,
∴PN=AM=BM=CM,PN∥BA,
PM=AN=DN=NE,PM∥AD,
∴AMPN是平行四边形,
∴∠BMP=∠PND,
∴∠PMC=∠ENP,
∴△PNE≌CMP(SAS),
∴CP=PE,
∵CM⊥AB,PN∥AB,
∴CM⊥PN,
∴CP⊥PE,
综上所述,CP=PE且CP⊥PE.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质,线段和差关系的证明方法、中点的用法、中位线性质等知识点,难度中等.对于证明线段和差关系的结论,截长或补短构造全等三角形是关键.第(3)问是中点的经典用法,取中点,借助中位线转移线段长度和角度,从而构造全等三角形,这一类题要引起重视.


科目:初中数学 来源: 题型:选择题
| A. | 0.1(精确到十分位) | B. | 0.05(精确到千分位) | ||
| C. | 0.05(精确到0.01) | D. | 0.052(精确到0.001) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最大的负数,没有最小的整数 | |
| B. | 没有最大的有理数,也没有最小的有理数 | |
| C. | 有最大的负数,没有最小的负数 | |
| D. | 有最小的负数,没有最大的正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
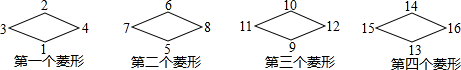
| A. | 第502个菱形的左边 | B. | 第502个菱形的右边 | ||
| C. | 第504个菱形的左边 | D. | 第503个菱形的右边 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com