
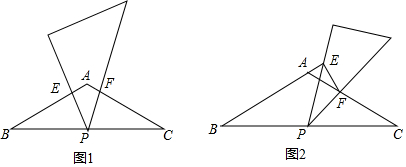
分析 (1)找出△BPE与△CFP的对应角,其中∠BPE+∠CPF=150°,∠CPF+∠CFP=150°,得出∠BPE=∠CFP,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明△BPE∽△PFE即可得出结论,③小题求出△BPE中BE上的高,求出△PEF中EF上的高,得出关系式
解答 (1)证明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似). (2)解:①△BPE∽△CFP;
(2)解:①△BPE∽△CFP;
理由::∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
②
同(1),可证△BPE∽△CFP,
∴$\frac{CP}{BE}=\frac{PF}{PE}$,而CP=BP,
∴$\frac{BP}{PF}=\frac{BE}{PE}$.
∵∠EBP=∠EPF,
∴△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
∴∠BEP=∠FEP,
∴EP平分∠BEF;
③由②得,∠BEP=∠PEF.
分别过点P作PM⊥BE,PN⊥EF,垂足分别为M、N,则PM=PN.
连AP,在Rt△ABP中,由∠B=30°,AB=8,可得AP=4.
∴PM=2$\sqrt{3}$,
∴PN=2$\sqrt{3}$,
∴S=S△EPF=$\frac{1}{2}$PN×EF=$\sqrt{3}$m.
点评 此题是相似形综合题,主要考查了等腰三角形的性质,相似三角形的判定和性质,三角形的面积公式,含30°的直角三角形的性质,判断三角形相似是解本题的关键,是一道中等难度的中考常考题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
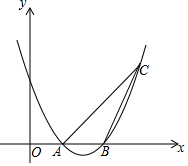 如图,抛物线y=x2-4x+3与x轴交于A,B两点,且过点C(4,3),在对称轴右侧的抛物线上是否存在点P,使∠PAC>∠ACB,若存在,求出点P的横坐标xP的取值范围;若不存在,请说明理由.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,且过点C(4,3),在对称轴右侧的抛物线上是否存在点P,使∠PAC>∠ACB,若存在,求出点P的横坐标xP的取值范围;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com