
【题目】某学校准备开展“阳光体有活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
各项目人数条形统计图 各项目人数扇形统计图


(1)这次活动一共调查了______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择乒乓球项目的人数所在扇形的圆心角等于_____度;
(4)若该学校有![]() 人,请你估计该学校选择足球项目的学生人数约是多少人.?
人,请你估计该学校选择足球项目的学生人数约是多少人.?
【答案】(1)250人;)(2)见解析;(3)57.6°;(4)480人.
【解析】
(1)直接利用足球人数÷所占百分比=总人数,即可得出答案;
(2)首先求出篮球人数进而补全条形统计图;
(3)利用(1)中所求,得出所占百分比进而得出答案;
(4)利用足球所占百分比进而估计总人数即可;
(1)由题意:![]() =250(人),
=250(人),
答:总共有250名学生;
(2)篮球人数:250-80-40-55=75(人),
如图所示: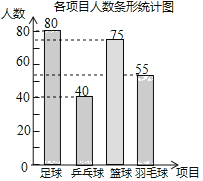
(3)依题意得:![]() ×360°=57.6°;
×360°=57.6°;
答:选择乒乓球项目的人数所在扇形的圆心角为57.6°;
(4)依题意得:1500×32%=480(人),
答:该学校选择足球项目的学生人数大约为480人;


科目:初中数学 来源: 题型:
【题目】如图是三阶幻方的一部分,其每行、每列、每条对角线上三个数字之和都相等,则对于这个幻方,下列说法错误的是( )

A. 每条对角线上三个数字之和等于![]()
B. 三个空白方格中的数字之和等于![]()
C. ![]() 是这九个数字中最大的数
是这九个数字中最大的数
D. 这九个数字之和等于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分6分)
(1)(3分)(-3)2-|-![]() |+(3.14-x)0
|+(3.14-x)0
(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB∥CD,点P是平面内直线AB、CD外一点连接PA、PC。
(1)写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系;
(2)证明图(1)和图(3)的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,-1)、B(2,0)、C(0,3),AC交![]() 轴于点D,AB交
轴于点D,AB交![]() 轴于点E.
轴于点E.
(1)△ABC的面积为________;
(2)点E的坐标为________;
(3)若点P的坐标为(0,![]() ):
):
①线段EP的长为________(用含![]() 的式子表示);
的式子表示);
②当![]() 时,求点P的坐标。
时,求点P的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
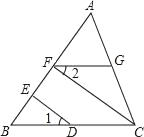
【题目】如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
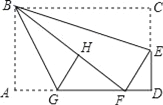
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com