
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,-1)、B(2,0)、C(0,3),AC交![]() 轴于点D,AB交
轴于点D,AB交![]() 轴于点E.
轴于点E.
(1)△ABC的面积为________;
(2)点E的坐标为________;
(3)若点P的坐标为(0,![]() ):
):
①线段EP的长为________(用含![]() 的式子表示);
的式子表示);
②当![]() 时,求点P的坐标。
时,求点P的坐标。

【答案】(1)面积为7;(2)E(0,-0.5);(3)①![]() ;②P(0,6.5),(0,-7.5).
;②P(0,6.5),(0,-7.5).
【解析】
(1)根据已知条件得到直线AC的解析式为y=2x+3,即可得到D(-![]() ,0),根据三角形的面积公式即可得到结论;
,0),根据三角形的面积公式即可得到结论;
(2)根据已知条件得到直线AB的解析式为y=![]() x-
x-![]() ,于是得到结论;
,于是得到结论;
(3)①根据点的坐标求得线段EP的长|-![]() -m|=|
-m|=|![]() +m|;
+m|;
②根据三角形的面积公式列方程即可得到结论.
解:(1)∵A(-2,-1)、C(0,3),
∴直线AC的解析式为y=2x+3,
∴当y=0时,x=-![]() ,
,
∴D(-![]() ,0),
,0),
∴△ABC的面积=![]() ×(2+
×(2+![]() )×(3+1)=7;
)×(3+1)=7;
(2)∵A(-2,-1)、B(2,0),
∴设直线AB的解析式为:y=kx+b,
∴![]() ,
,
∴ ,
,
∴y=![]() x-
x-![]() ,
,
∴E(0,-0.5);
(3)①∵点P的坐标为(0,m),
∴线段EP的长|-![]() -m|=|
-m|=|![]() +m|;
+m|;
②∵S△PAB=2S△ABC,
∴![]() ×|
×|![]() +m|×(2+2)=2×7,
+m|×(2+2)=2×7,
∴m=6.5或m=-7.5.
∴点P的坐标为:(0,6.5)或(0,-7.5)


科目:初中数学 来源: 题型:
【题目】边长为2![]() 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
(1)连接CQ,证明:CQ=AP;
(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE=![]() BC;
BC;
(3)猜想PF与EQ的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
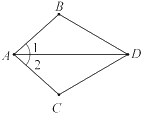
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
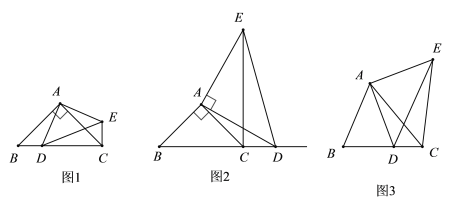
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
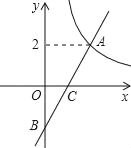
【题目】已知,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体有活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
各项目人数条形统计图 各项目人数扇形统计图


(1)这次活动一共调查了______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择乒乓球项目的人数所在扇形的圆心角等于_____度;
(4)若该学校有![]() 人,请你估计该学校选择足球项目的学生人数约是多少人.?
人,请你估计该学校选择足球项目的学生人数约是多少人.?
查看答案和解析>>
科目:初中数学 来源: 题型:
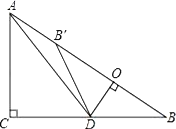
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
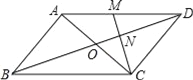
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
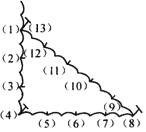
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com