
【题目】如图AB∥CD,点P是平面内直线AB、CD外一点连接PA、PC。
(1)写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系;
(2)证明图(1)和图(3)的结论。

【答案】(1)图1,∠APC+∠A+∠C=360°;图2,∠APC=∠A+∠C;图3,∠C=∠A+∠APC;图4,∠A=∠C+∠APC;(2)证明图1见解析;证明图3见解析.
【解析】
1)依据图形可得∠APC、∠PAB、∠PCD之间的数量关系;
(2)过P作PE∥AB,即可得到PE∥CD,再根据平行线的性质以及角的和差关系,即可得出∠PCD=∠CPE,∠PAB=∠APE,利用三角形的外角的性质,得出∠C=∠A+∠APC.
(1)图1,∠APC+∠A+∠C=360°;图2,∠APC=∠A+∠C;图3,∠C=∠A+∠APC;图4,A=∠C+∠APC.
(2)证明图1:

如图,过P点作,PE∥AB,则:∠A+∠APE=180°,
∵AB∥CD,
∴PE∥CD
∴∠EPC+∠C=180°.
又∵∠APC=∠APE+∠EPC,
∴∠APC+∠A+∠C=360°;
证明图3:过P作PE∥AB,
∵AB∥CD,
∴PE∥CD,
∴∠PCD=∠CPE,∠PAB=∠APE,
∴∠APC=∠CPE-∠APE=∠C-∠A,即∠C=∠A+∠APC


科目:初中数学 来源: 题型:
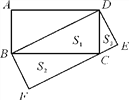
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1__ __S2+S3;(填“>”“=”或“<”)
(2)写出图中的三对相似三角形,并选择其中一对进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
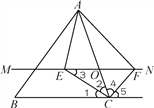
【题目】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连结AE、AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
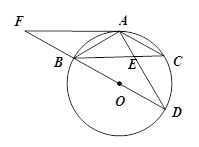
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
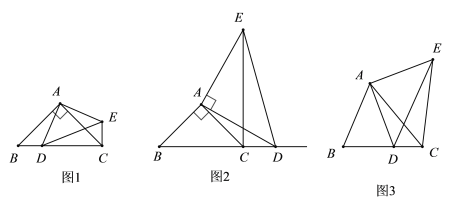
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体有活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
各项目人数条形统计图 各项目人数扇形统计图


(1)这次活动一共调查了______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择乒乓球项目的人数所在扇形的圆心角等于_____度;
(4)若该学校有![]() 人,请你估计该学校选择足球项目的学生人数约是多少人.?
人,请你估计该学校选择足球项目的学生人数约是多少人.?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°,∠D=31°,∠AED=143°,请你帮他判断该零件是否合格:___.(填“合格”或“不合格”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织1000名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机机取一些学生在评比中的成绩制成的统计图表如下:


根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a ,b ;
(2)补全频数分布表和频数分布直方图;
(3)如果评比成绩在95分以上(含95 分)的可以获得一等奖,试估计该校参加此次活动获得一等 奖的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com