Question

【题目】如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点.

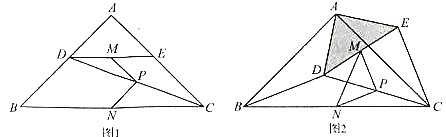
（1）观察猜想

图1中，线段与的数量关系是 ，位置关系是 ；

（2）探究证明

把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；

（3）拓展延伸

把绕点在平面内自由旋转，若，，请直接写出面积的最大值.

Answer 1

【答案】（1）PM=PN，；（2）等腰直角三角形，理由详见解析；（3）.

【解析】

试题分析：(1)已知 点，，分别为，，的中点，根据三角形的中位线定理可得,,,根据平行线的性质可得∠DPM=∠DCE，∠NPD=∠ADC，在中，，，，可得BD=EC，∠DCE+∠ADC=90°，即可得PM=PN，∠DPM+∠NPD=90°，即；（2）是等腰直角三角形，根据旋转的性质易证△BAD≌△CAE，即可得BD=CE，∠ABD=∠ACE，根据三角形的中位线定理及平行线的性质（方法可类比（1）的方法）可得PM=PN, ∠MPD=∠ECD，∠PNC=∠DBC，所以∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD，∠DPN=∠PNC+∠PCN =∠DBC+∠PCN，即可得∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°，即△PMN为等腰直角三角形；（3）把绕点旋转到如图的位置，此时PN=(AD+AB)=7, PM=(AE+AC)=7,且PN、PM的值最长，由（2）可知PM=PN，，所以面积的最大值为 .

试题解析：

（1）PM=PN，；

（2）等腰直角三角形，理由如下：

由旋转可得∠BAD=∠CAE，

又AB=AC,AD=AE

∴△BAD≌△CAE

∴BD=CE，∠ABD=∠ACE，

∵点，分别为，的中点

∴PM是△DCE的中位线

∴PM=CE，且,

同理可证PN=BD，且

∴PM=PN, ∠MPD=∠ECD，∠PNC=∠DBC，

∴∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD，

∠DPN=∠PNC+∠PCN =∠DBC+∠PCN，

∴∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°，

即△PMN为等腰直角三角形.

(3).