
����Ŀ���������¹涨������ͼ��G1��G2 �� ��PΪG1����һ�㣬��QΪG2����һ�㣬����߶�PQ�ij��ȴ�����Сֵ���ͳƸ���СֵΪ����ͼ��G1��G2֮��ľ��룮��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣮
��1����A������ΪA��1��0�������B��2��3��������OA֮��ľ���Ϊ �� ��C����2��3��������OA֮��ľ���Ϊ��
��2�����ֱ��y=x+1��˫����y= ![]() ֮��ľ���Ϊ
֮��ľ���Ϊ ![]() ����ôk=��������ͼ1�н����о���
����ôk=��������ͼ1�н����о���
��3����E������Ϊ��1�� ![]() ����������OE��ԭ��O˳ʱ����ת120�㣬�õ�����OF��������ƽ�������к�����OE��OF֮��ľ�����ȵĵ�����ɵ�ͼ�μ�Ϊͼ��M��
����������OE��ԭ��O˳ʱ����ת120�㣬�õ�����OF��������ƽ�������к�����OE��OF֮��ľ�����ȵĵ�����ɵ�ͼ�μ�Ϊͼ��M��
������ͼ2�л���ͼ��M��������ͼ��M����ɲ��֣������漰ƽ����ij������ʱ��������Ӱ��ʾ����
�ڽ�����OE��OF��ɵ�ͼ�μ�Ϊͼ��W��ֱ��y=��2x��4��ͼ��M�Ĺ������ּ�Ϊͼ��N�������ͼ��W��ͼ��N֮��ľ��룮
���𰸡�
��1��3��![]()
��2����4
��3��
�⣺����ͼ��x�������ᣬ��GOH�ı����ڲ������е㣨OH��OG�ֱ���OE��OF��ֱ����
 ��
��
���ɢ�֪OH����ֱ�߽���ʽΪy=�� ![]() x��OG����ֱ�߽���ʽΪy=
x��OG����ֱ�߽���ʽΪy= ![]() x��
x��
��  ��
��  ������M����
������M���� ![]() ��
�� ![]() ����
����
��  �ã�
�ã�  ������N����
������N���� ![]() ��
�� ![]() ����
����
�� ![]() ��x�ܩ�
��x�ܩ� ![]() ��
��
ͼ��N�����߶�MN���ϵ���������Ϊ��x����2x��4����
��ͼ��W��ͼ��N֮��ľ���Ϊd��
d= ![]()
= ![]()
= ![]()
�൱x=�� ![]() ʱ��d����СֵΪ
ʱ��d����СֵΪ ![]() =
= ![]() ��
��
��ͼ��W��ͼ��N֮��ľ��� ![]() ��
��
���������⣺��1���㣨2��3��������OA֮��ľ���Ϊ3���㣨��2��3��������OA֮��ľ���Ϊ ![]() =
= ![]() ��
��
�ʴ𰸷ֱ�Ϊ��3�� ![]() ��
��
����2����ֱ��y=x+1��˫����y= ![]() ֮��ľ���Ϊ
֮��ľ���Ϊ ![]() ��
��
��k��0������ֱ��y=x+1��˫����y= ![]() �ཻ������֮��ľ���Ϊ0����
�ཻ������֮��ľ���Ϊ0����
����O��ֱ��y=x+1�Ĵ���y=��x����˫����y= ![]() ���ڵ�E��F������E��EG��x�ᣬ��ͼ1��
���ڵ�E��F������E��EG��x�ᣬ��ͼ1��
�� ![]() ��
��  ������F����
������F���� ![]() ��
�� ![]() ����
����
��OF= ![]() =
= ![]() ��
��
��OE=OF+EF=2 ![]() ��
��
��Rt��OEG�У���EOG=��OEG=45�㣬OE=2 ![]() ��
��
����OG=EG= ![]() OE=2��
OE=2��
���E����������2��2����
��k=��2��2=��4��
�ʴ�Ϊ����4��
��1��ֻ������¶��弴�ɽ�����⣻��2������O��ֱ��y=x+1�Ĵ��ߣ���˫����y= ![]() ���ڵ�E��F������E��EG��x�ᣬ��ͼ1�������¶���ɵ�ֱ��y=��x��˫����y=
���ڵ�E��F������E��EG��x�ᣬ��ͼ1�������¶���ɵ�ֱ��y=��x��˫����y= ![]() ֮��ľ�������߶�EF�ij������ֻ�������E�����꣬���ô���ϵ�����Ϳ����k��ֵ����3���ٹ���O�ֱ�������OE��OF�Ĵ���OH��OG����ͼ2�������¶���ɵ�ͼ��MΪx��������ᡢ��GOH�ı����ڲ����еĵ㣻����ֱ��y=��2x��4������OH�Ľ���ΪM��������OG�Ľ���ΪN�������M��N�����꣬�ó�x�ķ�Χ����ͼ2��ͼ��N�ϵ���������Ϊ��x����2x��4���������¶���ɵ�ͼ��W��ͼ��N֮��ľ���Ϊd=
֮��ľ�������߶�EF�ij������ֻ�������E�����꣬���ô���ϵ�����Ϳ����k��ֵ����3���ٹ���O�ֱ�������OE��OF�Ĵ���OH��OG����ͼ2�������¶���ɵ�ͼ��MΪx��������ᡢ��GOH�ı����ڲ����еĵ㣻����ֱ��y=��2x��4������OH�Ľ���ΪM��������OG�Ľ���ΪN�������M��N�����꣬�ó�x�ķ�Χ����ͼ2��ͼ��N�ϵ���������Ϊ��x����2x��4���������¶���ɵ�ͼ��W��ͼ��N֮��ľ���Ϊd= ![]() ����Сֵ�����ö��κ��������������d=
����Сֵ�����ö��κ��������������d= ![]() ����Сֵ���Ϳɽ�����⣮
����Сֵ���Ϳɽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=4������P�ӵ�A������AC���յ�C�˶���ͬʱ����Q�ӵ�B������BA���A�˶�������A���������ԭ�����ٶ���AB���أ���P��Q�˶��ٶȾ�Ϊÿ��1����λ���ȣ�����P�����Cʱֹͣ�˶�����QҲͬʱֹͣ������PQ�����˶�ʱ��Ϊt��t��0���룮
��1���ڵ�Q��B��A���˶������У�
�ٵ�t=ʱ��PQ��AC��
��2�������APQ�����S����t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3��������P��Q������˶����߶�PQ�Ĵ�ֱƽ����Ϊl��
�ٵ�l������Aʱ������QP��AD�ڵ�E����AE�ij���
�ڵ�l������Bʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ƿ�ӵ��ݻ�Ϊ1 L��ƿ��װ����Һ����ƿ������ʱ��ƿ����Һ�ĸ߶�Ϊ20 cm����ƿ�ӵ���ʱ�����ಿ�ֵĸ߶�Ϊ5 cm.�ְ�ƿ�ڵ���Һȫ������һ��Բ���εı�������ڵ���Һ�߶�Ϊ10 cm.
��(1)ƿ����Һ�������
(2)Բ���α��ӵ��ڵ���뾶(��ȡ3.14�������ȷ��0.1 cm)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������һ��ʮ��·���������ɲ��ͣ�£�������ļ�ʻԱ������İ�����ǰ�����˵��ӽǷֱ��ǡ�DCA=30��͡�DCB=60�㣬��������ߵĿ�����AB=3�ף���ʻԱ�복ͷ�ľ�����0.8�ף���ʱ������ͷ������ߵľ���x�Ƕ��٣�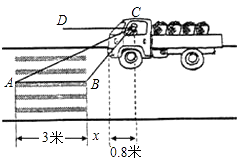
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�AB��ABC�ϣ���AE=BF=1��CE��DF�ཻ�ڵ�O�����н��ۣ� �١�DOC=90�㣬��OC=OE����tan��OCD= ![]() ���ܡ�COD����������ı���BEOF������У���ȷ���� �� ��
���ܡ�COD����������ı���BEOF������У���ȷ���� �� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y= ![]() x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
��1���������ߵĽ���ʽ��
��2������P����y��ƽ�е�ֱ��l��ֱ��AB��AC�ֱ��ڵ�E��F�����ı���AECP��������ʱ�����P�����ꣻ
��3������PΪ�����ߵĶ���ʱ����ֱ��AC���Ƿ���ڵ�Q��ʹ����C��P��QΪ��������������ABC���ƣ������ڣ������Q�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=�� ![]() x2+
x2+ ![]() x+3��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��E��
x+3��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��E��
��1���жϡ�ABC����״����˵�����ɣ�
��2������B��C�����ֱ�߽������ߵĶԳ����ڵ�D����PΪֱ��BC�Ϸ��������ϵ�һ���㣬����PCD��������ʱ��Q�ӵ�P�����������ʵ���·���˶��������ߵĶԳ����ϵ�M�������ش�ֱ�������߶Գ���ķ����˶���y���ϵĵ�N����������ʵ���·���˶�����A��ֹͣ������Q���˶�·�����ʱ�����N�����꼰��Q���������·���ij���
��3����ͼ2��ƽ�������ߣ�ʹ�����ߵĶ���E������AE���ƶ�����Eƽ�ƺ�Ķ�Ӧ��Ϊ��E�䣬��A�Ķ�Ӧ��Ϊ��A�䣬����AOC�Ƶ�O˳ʱ����ת����A1OC1��λ�ã���A��C�Ķ�Ӧ��ֱ�Ϊ��A1 �� C1 �� �ҵ�A1ǡ������AC�ϣ�����C1A�䣬C1E�䣬��A��C1E���Ƿ���Ϊ���������Σ����ܣ���������з��������ĵ�E������ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�B˳ʱ����ת����A1BO1��λ�ã�ʹ��A�Ķ�Ӧ��A1����ֱ��y= ![]() x�ϣ��ٽ���A1BO1�Ƶ�A1˳ʱ����ת����A1B1O2��λ�ã�ʹ��O1�Ķ�Ӧ��O2����ֱ��y=
x�ϣ��ٽ���A1BO1�Ƶ�A1˳ʱ����ת����A1B1O2��λ�ã�ʹ��O1�Ķ�Ӧ��O2����ֱ��y= ![]() x�ϣ����ν�����ȥ��������A�������ǣ�0��1������B�������ǣ�
x�ϣ����ν�����ȥ��������A�������ǣ�0��1������B�������ǣ� ![]() ��1�������A8�ĺ������� ��
��1�������A8������� �� 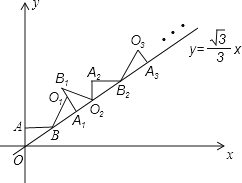
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com