Question

【题目】如图，已知抛物线y= x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．

（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵点A（0，1）．B（﹣9，10）在抛物线上，

∴ ，

∴ ，

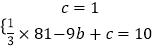∴抛物线的解析式为y= x2+2x+1，

（2）

解：∵AC∥x轴，A（0，1）

∴ x2+2x+1=1，

∴x1=﹣6，x2=0，

∴点C的坐标（﹣6，1），

∵点A（0，1）．B（﹣9，10），

∴直线AB的解析式为y=﹣x+1，

设点P（m， m2+2m+1）

∴E（m，﹣m+1）

∴PE=﹣m+1﹣（ m2+2m+1）=﹣ m2﹣3m，

∵AC⊥EP，AC=6，

∴S四边形AECP

=S△AEC+S△APC

= AC×EF+ AC×PF

= AC×（EF+PF）

= AC×PE

= ×6×（﹣ m2﹣3m）

=﹣m2﹣9m

=﹣（m+ ）2+ ，

∵﹣6＜m＜0

∴当m=﹣ 时，四边形AECP的面积的最大值是 ，

此时点P（﹣ ，﹣ ）．

（3）

解：∵y= x2+2x+1= （x+3）2﹣2，

∴P（﹣3，﹣2），

∴PF=yF﹣yP=3，CF=xF﹣xC=3，

∴PF=CF，

∴∠PCF=45°

同理可得：∠EAF=45°，

∴∠PCF=∠EAF，

∴在直线AC上存在满足条件的Q，

设Q（t，1）且AB=9 ，AC=6，CP=3

∵以C、P、Q为顶点的三角形与△ABC相似，

①当△CPQ∽△ABC时，

∴ ，

∴ ，

∴t=﹣4，

∴Q（﹣4，1）

②当△CQP∽△ABC时，

∴ ，

∴ ，

∴t=3，

∴Q（3，1）．

【解析】（1）用待定系数法求出抛物线解析式即可；（2）设点P（m， m2+2m+1），表示出PE=﹣ m2﹣3m，再用S四边形AECP=S△AEC+S△APC= AC×PE，建立函数关系式，求出极值即可；（3）先判断出PF=CF，再得到∠PCF=∠EAF，以C、P、Q为顶点的三角形与△ABC相似，分两种情况计算即可．
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．