
【题目】在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图. 
(1)已知点A的坐标为(1,0), ①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为 ![]() ,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
【答案】
(1)解:①∵A(1,0),B(3,1)
由定义可知:点A,B的“相关矩形”的底与高分别为2和1,
∴点A,B的“相关矩形”的面积为2×1=2;
②由定义可知:AC是点A,C的“相关矩形”的对角线,
又∵点A,C的“相关矩形”为正方形
∴直线AC与x轴的夹角为45°,
设直线AC的解析为:y=x+m或y=﹣x+n
把(1,0)分别y=x+m,
∴m=﹣1,
∴直线AC的解析为:y=x﹣1,
把(1,0)代入y=﹣x+n,
∴n=1,
∴y=﹣x+1,
综上所述,若点A,C的“相关矩形”为正方形,直线AC的表达式为y=x﹣1或y=﹣x+1;
(2)解:设直线MN的解析式为y=kx+b,
∵点M,N的“相关矩形”为正方形,
∴由定义可知:直线MN与x轴的夹角为45°,
∴k=±1,
∵点N在⊙O上,
∴当直线MN与⊙O有交点时,点M,N的“相关矩形”为正方形,
当k=1时,
作⊙O的切线AD和BC,且与直线MN平行,
其中A、C为⊙O的切点,直线AD与y轴交于点D,直线BC与y轴交于点B,
连接OA,OC,
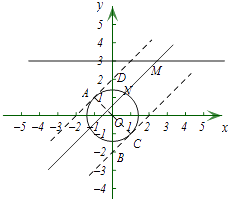
把M(m,3)代入y=x+b,
∴b=3﹣m,
∴直线MN的解析式为:y=x+3﹣m
∵∠ADO=45°,∠OAD=90°,
∴OD= ![]() OA=2,
OA=2,
∴D(0,2)
同理可得:B(0,﹣2),
∴令x=0代入y=x+3﹣m,
∴y=3﹣m,
∴﹣2≤3﹣m≤2,
∴1≤m≤5,
当k=﹣1时,把M(m,3)代入y=﹣x+b,
∴b=3+m,
∴直线MN的解析式为:y=﹣x+3+m,
同理可得:﹣2≤3+m≤2,
∴﹣5≤m≤﹣1;
综上所述,当点M,N的“相关矩形”为正方形时,m的取值范围是:1≤m≤5或﹣5≤m≤﹣1
【解析】(1)①由相关矩形的定义可知:要求A与B的相关矩形面积,则AB必为对角线,利用A、B两点的坐标即可求出该矩形的底与高的长度,进而可求出该矩形的面积;②由定义可知,AC必为正方形的对角线,所以AC与x轴的夹角必为45,设直线AC的解析式为;y=kx+b,由此可知k=±1,再(1,0)代入y=kx+b,即可求出b的值;(2)由定义可知,MN必为相关矩形的对角线,若该相关矩形的为正方形,即直线MN与x轴的夹角为45°,由因为点N在圆O上,所以该直线MN与圆O一定要有交点,由此可以求出m的范围.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1)在点Q从B到A的运动过程中,
①当t=时,PQ⊥AC;
(2)②求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l.
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,下图是根据调查结果绘制的两幅不完整的统计图. 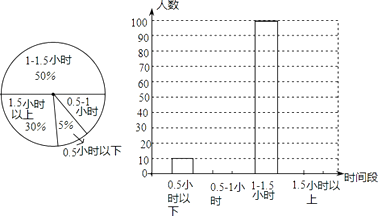
请你根据统计图提供的信息,解答以下问题:
(1)“平均每天参加体育活动的时间”“为0.5~1小时”部分的扇形统计图的圆心角为度;
(2)本次一共调查了名学生;
(3)将条形统计图补充完整;
(4)若该校有2000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个瓶子的容积为1 L,瓶内装着溶液,当瓶子正放时,瓶内溶液的高度为20 cm,当瓶子倒放时,空余部分的高度为5 cm.现把瓶内的溶液全部倒在一个圆柱形的杯子里,杯内的溶液高度为10 cm.
求:(1)瓶内溶液的体积;
(2)圆柱形杯子的内底面半径(π取3.14,结果精确到0.1 cm).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?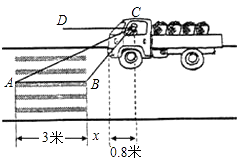
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
A.60
B.80
C.30
D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com