
(本题满分12分)如图1,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴 于A、B两点,交y轴C、D于两点,且C为弧AE的中点,AE交y轴于点G,若A点的坐标为(-2,0),CD=8
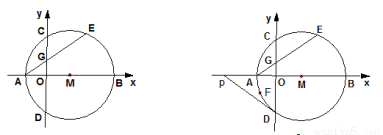
(1)求⊙M的半径
(2)求AE的长
(3)如图2,过点D作⊙M的切线,交x轴于点P.动点F在⊙M圆周上运动时,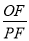 的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
的比值是否发生变化,若不变,求出比值:若不变,请说明变化规律
见解析
【解析】
试题分析:(1)连结CM,则AB CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,根据勾股定理可得r=5;(2)因为AB
CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,根据勾股定理可得r=5;(2)因为AB CD,所以弧AC=弧AD,又C为弧AE的中点,所以可证弧CD=弧AE,所以AE=CD=8;(3)连结AM,利用△MOD∽△MDP, △MOD∽△DOP可得OP=
CD,所以弧AC=弧AD,又C为弧AE的中点,所以可证弧CD=弧AE,所以AE=CD=8;(3)连结AM,利用△MOD∽△MDP, △MOD∽△DOP可得OP=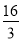 ,然后分三种情况讨论:点F与点A重合,点F与点B重合,点F与点A、B都不重合,可求出
,然后分三种情况讨论:点F与点A重合,点F与点B重合,点F与点A、B都不重合,可求出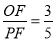 .
.
试题解析:(1)连结CM,则AB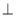 CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,
CD,所以OC=0D=4,设⊙M的半径为r,A点的坐标为(-2,0),所以OM=r-2,在Rt△OCM中,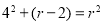 ,所以r=5;(2)因为AB
,所以r=5;(2)因为AB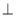 CD,所以弧AC=弧AD,又C为弧AE的中点,所以弧CD=弧AE,所以AE=CD=8;(3)如图2,连结AM,则DM
CD,所以弧AC=弧AD,又C为弧AE的中点,所以弧CD=弧AE,所以AE=CD=8;(3)如图2,连结AM,则DM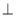 PD, DO
PD, DO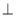 PM,所以△MOD∽△MDP, △MOD∽△DOP ,所以
PM,所以△MOD∽△MDP, △MOD∽△DOP ,所以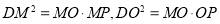 ,所以
,所以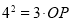 ,所以OP=
,所以OP=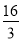 ,然后分三种情况讨论:点F与点A重合时,
,然后分三种情况讨论:点F与点A重合时, ,点F与点B重合时,
,点F与点B重合时, ,点F与点A、B都不重合时,
,点F与点A、B都不重合时,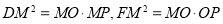 ,所以
,所以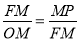 ,因为∠AMF=∠MPF,所以△MFO∽△MPF,所以
,因为∠AMF=∠MPF,所以△MFO∽△MPF,所以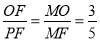 .综上所述
.综上所述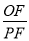 的值不变,值为
的值不变,值为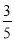 .
.
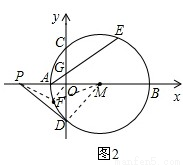
考点:1.垂径定理;2.勾股定理;3.相似三角形的判定与性质.


科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:填空题
平面直角坐标系内Rt△ABO的顶点A坐标为(5,4),将△ABO绕O点逆时针旋转90°后,顶点A的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:选择题
抛物线y=2(x-2)2+3的顶点坐标是 ( )
A.(-2,3) B.(2,3) C.(-1,3) D.(1,3)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:选择题
若关于x的一元二次方程(k-1)x2+x-k2=0的一个根为1,则k的值为( )
A.-1 B.0或1 C.1 D.0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:填空题
在一暗箱中,装有a个白色乒乓球和10个黄色乒乓球,每次搅拌均匀后,任意摸出一个球后放回,这时摸到黄球的概率40%,则a= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:解答题
(本题满分8分)某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均的每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 万元.
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:填空题
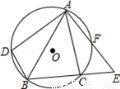
如图,△ABC内接于⊙O,D是弧AB上一点,E是BC的延长线上一点,AE交⊙O于点F,
若要使△ADB∽△ACE,还需添加一个条件,这个条件可以是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广西省九年级12月月考数学试卷(解析版) 题型:解答题
某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件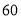 元.经市场调研发现:该款工艺品每天的销售量
元.经市场调研发现:该款工艺品每天的销售量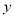 件与售价
件与售价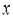 元之间存在着如下表所示的一次函数关系.
元之间存在着如下表所示的一次函数关系.
售价 | … |
|
| … |
销售量 | … |
|
| … |
(1)求销售量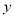 件与售价
件与售价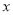 元之间的函数关系式;
元之间的函数关系式;
(2)设每天获得的利润为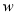 元,当售价
元,当售价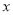 为多少时,每天获得的利润最大?并求出最大值.
为多少时,每天获得的利润最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市永定丰田片区九年级上学期第三次月考数学试卷(解析版) 题型:选择题
如果将抛物线y=x2向左平移2个单位,那么所得抛物线的表达式为( )
A、y=x2+2
B、y=x2-2
C、y=(x+2)2
D、y=(x-2)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com