
| A. | 图象经过点(1,-3) | |
| B. | 图象分布在第二、四象限 | |
| C. | 当x>0时,y随x的增大而增大 | |
| D. | 点A(x1,y1)、B(x2、y2)都在反比例函数y=-$\frac{3}{x}$的图象上,若x1<x2,则y1<y2 |
分析 根据反比例函数图象的性质对各选项分析判断后利用排除法求解.
解答 解:A、∵-$\frac{3}{1}$=-3,∴点(1,-3)在它的图象上,故本选项正确;
B、k=-3<0,∴它的图象在第二、四象限,故本选项正确;
C、k=-3<0,当x>0时,y随x的增大而增大,故本选项正确;
D、点A(x1,y1)、B(x2、y2)都在反比例函数y=-$\frac{3}{x}$的图象上,若x1<x2<0,则y1<y2,故本选项错误.
故选D.
点评 本题考查了反比例函数的性质,对于反比例函数y=$\frac{k}{x}$(k≠0),(1)k>0,反比例函数图象在一、三象限,在每一个象限内,y随x的增大而减小;(2)k<0,反比例函数图象在第二、四象限内,在每一个象限内,y随x的增大而增大.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
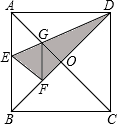 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
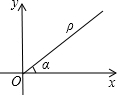 如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (2,-2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,-2) | D. | (-4,-4$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com