

分析 连接AP,当点P在底边BC上时,根据等腰三角形的性质可表示出S△ABC=S△ABP+S△ACP=$\frac{1}{2}$×AC×(PD+PE),同时可表示出S△ABC=$\frac{1}{2}$AC×BF,从而可得到PD+PE=BF.,当点P在底边的延长线上时,根据S△APB=S△ABC+S△ACP进行推理,证法同(1).
解答 解:①如图1,连接AP.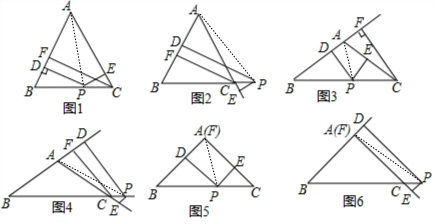
∵AB=AC,
∴S△ABC=S△ABP+S△ACP=$\frac{1}{2}$AB×PD+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(PD+PE),
∵S△ABC=$\frac{1}{2}$AB×CF,
∴PD+PE=CF.
②如图2,连接AP
∵AB=AC,
∴S△APB=S△ABC+S△ACP=$\frac{1}{2}$AB×CF+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(CF+PE),
∵S△APB=$\frac{1}{2}$AB×PD,
∴CF+PE=PD,即PD-PE=CF;
③如图3,连接AP,
∵AB=AC,
∴S△ABC=S△ABP+S△ACP=$\frac{1}{2}$AB×PD+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(PD+PE),
∵S△ABC=$\frac{1}{2}$AB×CF,
∴PD+PE=CF.
④如图4,连接AP,
∵AB=AC,
∴S△APB=S△ABC+S△ACP=$\frac{1}{2}$AB×CF+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(CF+PE),
∵S△APB=$\frac{1}{2}$AB×PD,
∴CF+PE=PD,即PD-PE=CF;
⑤如图5,连接AP,
∵AB=AC,
∴S△ABC=S△ABP+S△ACP=$\frac{1}{2}$AB×PD+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(PD+PE),
∵S△ABC=$\frac{1}{2}$AB×CF,
∴PD+PE=CF.
⑥如图6,连接AP,
∵AB=AC,
∴S△APB=S△ABC+S△ACP=$\frac{1}{2}$AB×CF+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(CF+PE),
∵S△APB=$\frac{1}{2}$AB×PD,
∴CF+PE=PD,即PD-PE=CF;
得出规律:,无论等腰三角形是锐角三角形、钝角三角形或直角三角形,
当点P在等腰三角形的地边上时,点P到两腰的距离之和等于一腰上的高;
当点P在底边的延长线上时,点P到两腰的距离之差等于一腰上的高.
点评 此题主要考查等腰三角形的性质及三角形面积的综合运用,此题的关键是利用面积公式将所求联系在一起.


科目:初中数学 来源: 题型:选择题
| A. | 调查新泰市市民的吸烟情况 | |
| B. | 调查中央电视台某节目的收视率 | |
| C. | 调查新泰市市民家庭日常生活支出情况 | |
| D. | 调查新泰市市某校某班学生对“新泰市创建文明城市活动”的知晓率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3米 | B. | $\frac{6\sqrt{5}}{5}$米 | C. | 2$\sqrt{3}$米 | D. | $\frac{12\sqrt{5}}{5}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(1,-3) | |
| B. | 图象分布在第二、四象限 | |
| C. | 当x>0时,y随x的增大而增大 | |
| D. | 点A(x1,y1)、B(x2、y2)都在反比例函数y=-$\frac{3}{x}$的图象上,若x1<x2,则y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
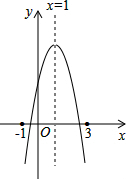 如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )
如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com