
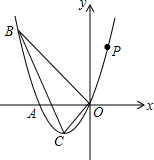
 ��ͼ����֪�����߾�����A��-2��0������B��-3��3����ԭ��O������ΪC��
��ͼ����֪�����߾�����A��-2��0������B��-3��3����ԭ��O������ΪC������ ��1�����������߹�A��-2��0����ԭ�����y=a��x+2����x-0����Ȼ�����������y=a��x+2����x-0����B��-3��3�������a��ֵ���ɣ�
��2������һ��G��ʹ�á�GBC��������G��GH��ֱy�ύBC�ڵ�H����G��x1��x2+2x�������ֱ��BC�Ľ���ʽΪy=kx+b�������ֱ�ߵĽ���ʽ�������ɱ�ʾ����H�����꣬���������ε������ʽ�ɵõ���GBC�������x�ĺ�����ϵ���ɺ��������ʼ��������������ֵ�Լ���G�����ꣻ
��3���������⻭��ͼ�Σ�����B������Ϊ-3�����������߽���ʽ��������꣬ȷ����B���꣬�������BC��BO��OC�ij������ù��ɶ������涨���õ�������BOCΪֱ�������Σ���P��M��AΪ��������������BOC���ƣ���P��m��n�����������m��0��n��0����n=m2+2m���������Ƶñ������г�����m�ķ��̣�������̵Ľ�õ�m��ֵ���������n��ֵ������ȷ����P�����ꣻ
��4��������������ǣ�D�ڵ�һ���ޣ��ڶ������Լ��������ޣ�����ƽ���ı��ε����ʼ�������ͼ���������D���꼴�ɣ�
��� �⣺��1�����������߹�A��-2��0����ԭ�㣬����y=a��x+2����x-0����
�֡�������y=a��x+2��x��B��-3��3����
��-3��-3+2��a=3��
��a=1��
�������ߵĽ���ʽΪy=��x+2��x=x2+2x��
��2������һ��G��ʹ�á�GBC���������������£�
���ɣ���G��GH��ֱy�ύBC�ڵ�H����G��x1��x2+2x�������ֱ��BC�Ľ���ʽΪy=kx+b��
��y=��x-2��x=x2-2x=��x+1��2-1��
�ඥ��C��-1��-1����
�֡�B��-3��3����
��$\left\{\begin{array}{l}{-k+b=-1}\\{-3k+b=3}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=-2}\\{b=-3}\end{array}\right.$��
��y=-2x-3��
������H��x��-2x-3��
��S��GBC=$\frac{1}{2}$��-2x-3-x2-2x��•��-1+3��=-x2-4x-3=-��x+2��2+1
��a=-1��0���Գ���Ϊx=-2��
�൱x=-2ʱ��S��GBC=1���ʱ��G��-2��0����
��3�����ڣ�
�ߵ�B���������ϣ�
�൱x=-3ʱ��y=9-6=3��
��B��-3��3����
���ݹ��ɶ����ã�BO2=9+9=18��CO2=1+1=2��BC2=16+4=20��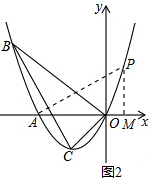
��BO2+CO2=18+2=20��
��BO2+CO2=BC2��
���BOCΪֱ�������Σ�
������ڵ�P��ʹ����P��M��AΪ��������������BOC���ƣ���ͼ2��
��P��m��n�����������m��0��n��0����n=m2+2m��
������AMP�ס�BOC����$\frac{AM}{BO}=\frac{PM}{CO}$����$\frac{m+2}{\sqrt{18}}=\frac{{m}^{2}+2m}{\sqrt{2}}$��
�����ã�m+2=3��m2+2m��=0����3m2+5m-2=0��
��ã�m1=$\frac{1}{3}$��m2=-2����ȥ����
m1=$\frac{1}{3}$ʱ��n=$\frac{1}{9}$+$\frac{2}{3}$=$\frac{7}{9}$��
��P��$\frac{1}{3}$��$\frac{7}{9}$����
������AMP�ס�COB����$\frac{AM}{CO}=\frac{PM}{BO}$����$\frac{m+2}{\sqrt{2}}=\frac{{m}^{2}+2}{\sqrt{18}}$��
�����ã�m2-m-6=0��
��� m1=3��m2=-2����ȥ����
��m=3ʱ��n=9+6=15��
��P��3��15����
�������������������ĵ�P���������ֱ���P1��$\frac{1}{3}$��$\frac{7}{9}$����P2��3��15����
��4����ͼ3��ʾ��������������ǣ�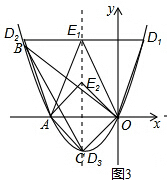
��D1�ڵ�һ����ʱ�����ı���AOD1E1Ϊƽ���ı��Σ�
��AO=E1D1=2��
�������߶Գ���Ϊֱ��x=-1��
��D1������Ϊ1��
��x=1����������y=x2+2x=1+2=3����D1��1��3����
��D2�ڵڶ�����ʱ��ͬ��D2��-3��3����
��D3�ڵ�������ʱ�����ı���AE2OD3Ϊƽ���ı��Σ���ʱD3��C�غϣ���D3��-1��-1����
���� �����ۺϿ����˶��κ������ۺϣ��ô���ϵ��������κ����Ľ���ʽ�����������ε����ʺ��ж������ɶ������涨����ƽ���ı��ε��ж���֪ʶ���Ӧ�ã������ۺ��ԱȽ�ǿ����һ�����Ѷȣ���ѧ������ϸߵ�Ҫ��ע�⣺��Ҫ©�⣬��������˼����������ã�


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��5�� | B�� | ��-8��5�� | C�� | ��-8��-1�� | D�� | ��2��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
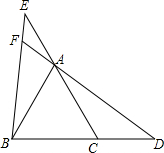 ��ͼ����ABC�ǵȱ������Σ���D��E�ֱ���BC��CA�ӳ����ϵĵ㣬��CD=AE��DA���ӳ��߽�BE�ڵ�F��
��ͼ����ABC�ǵȱ������Σ���D��E�ֱ���BC��CA�ӳ����ϵĵ㣬��CD=AE��DA���ӳ��߽�BE�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com