Question

【题目】在边长为1的正方形网格中标有A、B、C、D、E、F六个格点，顶点在格点上的三角形叫做格点三角形，如格点三角形△ABC．

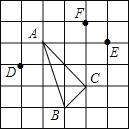
（1）△ABC的面积为　 　；

（2）△ABC的形状为　 　；

（3）根据图中标示的各点（A、B、C、D、E、F）位置，与△ABC全等的格点三角形是　 　．

Answer 1

【答案】（1）2；（2）直角三角形；（3）△DBC，△DAB，△DAC．

【解析】

（1）用三角形ABC所在的长方形的面积减去四周的三个三角形的面积即可得；

（2）利用勾股定理分别求出三角形ABC的边长，再利用勾股定理的逆定理进行判断即可；

（3）已知△ABC的各边长，根据网格的特征以及全等三角形的性质可得.

（1）△ABC的面积为：2×3﹣﹣﹣＝2，

故答案为：2；

（2）由勾股定理得：AC＝＝2，BC＝＝，AB＝＝，

所以AC2+BC2＝AB2，

即∠ACB＝90°，

即△ABC是直角三角形，

故答案为：直角三角形；

（3）与△ABC全等的格点三角形是△DBC，△DAB，△DAC，

故答案为：△DBC，△DAB，△DAC．