
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x+2与x轴相交于点A、B,交y轴于点C,抛物线的对称轴交x轴于点N,交线段AC于点M.点F是线段MA上的动点,连接NF,过点N作NG⊥NF交△ABC的边于点G.
x+2与x轴相交于点A、B,交y轴于点C,抛物线的对称轴交x轴于点N,交线段AC于点M.点F是线段MA上的动点,连接NF,过点N作NG⊥NF交△ABC的边于点G.
(1)求证:△ABC是直角三角形;
(2)当点G在边BC上时,连接GF,∠NGF的度数变化吗?若变化,请说明理由;若不变,请求出∠NGF的正切值;
(3)设点F的横坐标为n,点G的纵坐标为m,在整个运动过程中,直接写出m与n的函数关系式,并注明自变量n的取值范围.

【答案】(1)证明见解析;(2)∠NGF的度数不变化,tan∠NGF=![]() ;(3)m与n的关系式为:m=2n–3(
;(3)m与n的关系式为:m=2n–3(![]() ≤n≤
≤n≤![]() )或m=
)或m=![]() (
(![]() <n≤4).
<n≤4).
【解析】(1)先利用抛物线解析式确定A、B、C的坐标,然后利用勾股定理的逆定理进行证明即可;
(2)先利用待定系数法求出直线AC的然后式,则可确定M(![]() ,
,![]() ),再证明△NMF∽△NBG,利用相似比得到
),再证明△NMF∽△NBG,利用相似比得到![]() =
=![]() ,然后根据正切的定义得到tan∠NGF
,然后根据正切的定义得到tan∠NGF![]() ,从而判断∠NGF的度数为定值;
,从而判断∠NGF的度数为定值;
(3)作GH⊥x轴于H,FQ⊥x轴于Q,F(n,–![]() n+2),分点G在BC上,点G在AC上两种情况进行讨论即可得.
n+2),分点G在BC上,点G在AC上两种情况进行讨论即可得.
(1)当x=0时,y=–![]() x2+
x2+![]() x+2=2,则C(0,2);
x+2=2,则C(0,2);
当y=0时,–![]() x2+
x2+![]() x+2=0,解得x1=–1,x2=4,则A(4,0),B(–1,0),(2分)
x+2=0,解得x1=–1,x2=4,则A(4,0),B(–1,0),(2分)
∵BC2=12+22=5,AC2=42+22=20,AB2=25,
∴BC2+AC2=AB2,
∴△ABC为直角三角形,∠ACB=90°;
(2)∠NGF的度数不变化,
设直线AC的解析式为y=kx+b,
把A(4,0),C(0,2)代入得![]() ,解得
,解得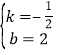 ,
,
∴直线AC的解析式为y=–![]() x+2,
x+2,
∵抛物线的对称轴为直线x=![]() ,∴M(
,∴M(![]() ,
,![]() ),
),
∵GN⊥NF,∴∠GNF=90°,∴∠BNG=∠MNF,
∵∠ACB=90°,∴∠NBC=∠OCA,而MN∥OC,
∴∠NMF=∠OCA,∴∠NBG=∠NMF,∴△NMF∽△NBG,
∴![]() =
=![]() =
=![]() ,∴tan∠NGF=
,∴tan∠NGF=![]() ,
,
∴∠NGF的度数为定值;
(3)作GH⊥x轴于H,FQ⊥x轴于Q,F(n,–![]() n+2),
n+2),
当G点在BC上,如图1,易得直线BC的解析式为y=2x+2,
则G(![]() m–1,m),
m–1,m),
∵∠GNF=90°,∴∠GNH=∠NFQ,∴Rt△NGH∽Rt△FNQ,
∴![]() ,即
,即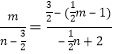 ,
,
∴m=2n–3,
当m=0时,2n–3=0,解得n=![]() ;当m=2时,2n–3=2,解得n=
;当m=2时,2n–3=2,解得n=![]() ;
;
∴此时n的范围为![]() ≤n≤
≤n≤![]() ;
;

当点G在AC上,如图2,则![]() <n≤4,则G(4–2m,m),
<n≤4,则G(4–2m,m),
易得Rt△NGH∽Rt△FNQ,
∴![]() ,即
,即 ,∴m=
,∴m=![]() ,
,
综上所述,故答案为:m与n的关系式为:m=2n–3(![]() ≤n≤
≤n≤![]() )或m=
)或m=![]() (
(![]() <n≤4).
<n≤4).


科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化为一元二次方程的一般形式
的方程,并将其化为一元二次方程的一般形式
(1)有一个三位数,它的个位数字比十位数字大![]() ,十位数字比百位数字小
,十位数字比百位数字小![]() ,三个数字的平方和的
,三个数字的平方和的![]() 倍比这个三位数小
倍比这个三位数小![]() ,求这个三位数.
,求这个三位数.
(2)如果一个直角三角形的两条直角边长之和为![]() ,面积为
,面积为![]() ,求它的两条直角边的长.
,求它的两条直角边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,实验数据如下表:
摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是 .
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,设甲每天加工x个玩具:
(1)乙每天加工 个玩具(用含x的代数式表示);
(2)求甲乙两人每天各加工多少个玩具?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,顶点在格点上的三角形叫做格点三角形,如格点三角形△ABC.
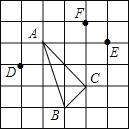
(1)△ABC的面积为 ;
(2)△ABC的形状为 ;
(3)根据图中标示的各点(A、B、C、D、E、F)位置,与△ABC全等的格点三角形是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①图象经过点(1,﹣3);②关于x的方程kx+b=0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y<0.其中正确的是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为64,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
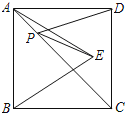
A.6B.8C.9D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com