
【题目】已知:抛物线y= ![]() (x﹣1)2﹣3.
(x﹣1)2﹣3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
【答案】
(1)解:抛物线y= ![]() (x﹣1)2﹣3,
(x﹣1)2﹣3,
∵a= ![]() >0,
>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)解:∵a= ![]() >0,
>0,
∴函数y有最小值,最小值为﹣3;
(3)解:令x=0,则y= ![]() (0﹣1)2﹣3=﹣
(0﹣1)2﹣3=﹣ ![]() ,
,
所以,点P的坐标为(0,﹣ ![]() ),
),
令y=0,则 ![]() (x﹣1)2﹣3=0,
(x﹣1)2﹣3=0,
解得x1=﹣1,x2=3,
所以,点Q的坐标为(﹣1,0)或(3,0),
当点P(0,﹣ ![]() ),Q(﹣1,0)时,设直线PQ的解析式为y=kx+b(k≠0),
),Q(﹣1,0)时,设直线PQ的解析式为y=kx+b(k≠0),
则 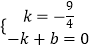 ,
,
解得 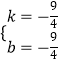 ,
,
所以直线PQ的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
当P(0,﹣ ![]() ),Q(3,0)时,设直线PQ的解析式为y=mx+n,
),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则 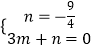 ,
,
解得 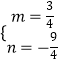 ,
,
所以,直线PQ的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
综上所述,直线PQ的解析式为y=﹣ ![]() x﹣
x﹣ ![]() 或y=
或y= ![]() x﹣
x﹣ ![]() .
.
【解析】(1)根据二次函数的性质,写出开口方向与对称轴即可;(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;(3)分别求出点P、Q的坐标,再根据待定系数法求函数解析式解答.
【考点精析】通过灵活运用确定一次函数的表达式和二次函数的性质,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】(c2012防城港)某奶品生产企业,2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计,绘制了图1、2的统计图,请根据图中信息解答下列问题: 
(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2所对应的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A的坐标为(﹣2,﹣1),点B的坐标为(0,﹣2),若将线段AB平移至A′B′的位置,点A′的坐标为(a,2),点B′的坐标为(1,b),则a+b的值为( )
A. 0 B. 2 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=4,BC=12,点E是BC的中点.点P、Q分别是边AD、BC上的两点,其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A,同时点Q以每秒2个单位长度的速度从点C出发向点B运动.当其中一点到达终点时停止运动.当运动时间t为_____秒时,以点A、P,Q,E为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表反映了x与y之间存在某种函数关系,现给出了几种可能的函数关系式: y=x+7,y=x﹣5,y=﹣ ![]() ,y=
,y= ![]() x﹣1
x﹣1
x | … | ﹣6 | ﹣5 | 3 | 4 | … |
y | … | 1 | 1.2 | ﹣2 | ﹣1.5 | … |
(1)从所给出的几个式子中选出一个你认为满足上表要求的函数表达式:;
(2)请说明你选择这个函数表达式的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2017年12月份的日历.如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:7×9﹣1×15= ,18×20﹣12×26= ,不难发现,结果都是 .

(1)请将上面三个空补充完整;
(2)我们发现选择其他类似的部分规律也相同,请你利用整式的运算对以上的规律加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
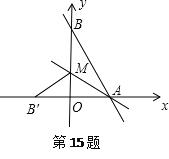
【题目】如图,直线y=﹣![]() x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com