
 如图是用4个相同的小长方形与1个小正方形镶嵌而成的图案,已知该图案的面积为25,小正方形的面积为4,若用x,y表示小长方形的两邻边长(x>y),则下列关系中不正确的是( )
如图是用4个相同的小长方形与1个小正方形镶嵌而成的图案,已知该图案的面积为25,小正方形的面积为4,若用x,y表示小长方形的两邻边长(x>y),则下列关系中不正确的是( )| A. | x+y=5 | B. | y-x=2 | C. | 4xy+4=25 | D. | y2+x2=25 |
分析 本题中正方形图案的边长7,同时还可用(x+y)来表示,其面积从整体看是25,从组合来看,可以是(x+y)2,还可以是(4xy+4),接下来,我们再灵活运用等式的变形,即可作出判断.
解答 解:A、因为正方形图案的边长5,同时还可用(x+y)来表示,故x+y=5正确;
B、因为正方形图案面积从整体看是25,
从组合来看,可以是(x+y)2,还可以是(4xy+4),
所以有(x+y)2=25,4xy+4=25
即xy=$\frac{21}{4}$,
所以(x-y)2=(x+y)2-4xy=25-21=4,
即x-y=2;
C、由B可知4xy+4=25,正确;
D、x2+y2=(x+y)2-2xy=25-2×$\frac{21}{4}$=$\frac{29}{2}$,故x2+y2=25是错误的.
故选D.
点评 本题考查整式的混合计算,关键是结合图形,利用等式的变形来解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+2与x轴交于A、B两点,与y轴交于C点.
已知抛物线y=-x2+2与x轴交于A、B两点,与y轴交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
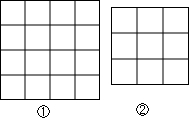 如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是有几个小立方体块搭建成的几何体的俯视图,小正方体中的数字表示在该位置小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
如图是有几个小立方体块搭建成的几何体的俯视图,小正方体中的数字表示在该位置小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
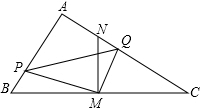 如图,在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,M是BC边的中点,MN⊥BC交AC于点N.直角∠PMQ绕顶点M旋转,使得边MP于线段BA交于点P,边MQ与线段AC交于点Q.
如图,在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,M是BC边的中点,MN⊥BC交AC于点N.直角∠PMQ绕顶点M旋转,使得边MP于线段BA交于点P,边MQ与线段AC交于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com