
【题目】如图,![]() 为
为![]() 的角平分线,
的角平分线,![]() ,
,![]() 在
在![]() 延长线上,且
延长线上,且![]() ,若
,若![]() ,则
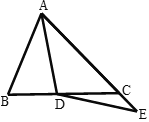
,则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
过点D作DF//AB,交AC于点F,根据已知条件易证AF=BD=FD,再证明△ABD△EFD,得到AB=EF=6,即可得CF=4;由DF//AB,可得△CDF ΔCBA,根据相似三角形的性质可得![]() ,即可得
,即可得![]() ,由此求得BD即可.
,由此求得BD即可.
过点D作DF//AB,交AC于点F,
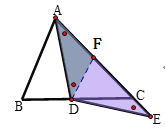
∴∠DFC=∠BAC,∠ABC=∠FDC,
∵AC=BC,
∴∠BAC=∠ABC,
∴∠DFC =∠FDC,
∴CD=CF,
∴BD=AF;
∵AD为△ABC的角平分线,
∴∠BAD=∠DAC,
∵AD=DE,
∴∠DAE=∠DEA,
∴∠BAD=∠DEF,
在△ABD和△EFD中,
∠BAD=∠DEF,∠ABD=∠EFD,AD=DE,
∴△ABD△EFD,
∴AB=EF=6,
∴CF=4,
∵DF//AB,
∴∠ADF=∠BAD,
∵∠BAD=∠DAC,
∴∠ADF=∠DAF,
∴AF=DF,
∴AF=DF=BD,
∵DF//AB,
∴△CDF ΔCBA,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
解得BD=![]() 或BD=
或BD=![]() (舍去),
(舍去),
∴BD=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
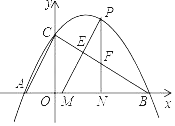
【题目】如图,二次函数y=ax2+bx+![]() 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)求这个二次函数的解析式;
(2)求线段PE最大值,并求出线段PE最大时点P的坐标;
(3)若S△PMN=3S△PEF时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
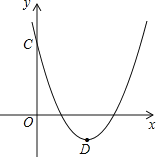
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
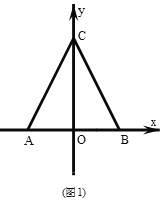
【题目】已知:在平面直角坐标系中,![]() 为坐标原点,直线
为坐标原点,直线![]() 分别交
分别交![]() 轴负半轴和
轴负半轴和![]() 轴正半轴于
轴正半轴于![]() 两点,将
两点,将![]() 沿
沿![]() 轴翻折至
轴翻折至![]() ,且
,且![]() 的面积为8.
的面积为8.
(1)如图,求直线![]() 的解析式;
的解析式;
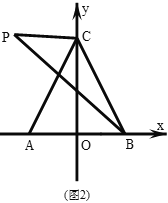
(2)如图,点![]() 为第二象限内
为第二象限内![]() 上方的一点,连接
上方的一点,连接![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式(用含
的函数关系式(用含![]() 的代数式表示);
的代数式表示);
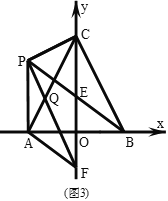
(3)如图,在(2)的条件下,连接![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,且
,且![]() ,求点
,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
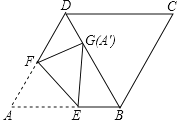
【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象记作
的图象记作![]() ,一次函数
,一次函数![]() 的图象记作
的图象记作![]() ,对于这两个图象,有以下几种说法:
,对于这两个图象,有以下几种说法:
①当![]() 与
与![]() 有公共点时,
有公共点时,![]() 随
随![]() 增大而减小;
增大而减小;
②当![]() 与
与![]() 没有公共点时,
没有公共点时,![]() 随
随![]() 增大而增大;
增大而增大;
③当![]() 时,
时,![]() 与
与![]() 平行,且平行线之间的距离为
平行,且平行线之间的距离为![]() .
.
下列选项中,描述准确的是( )
A. ①②正确,③错误B. ①③正确,②错误
C. ②③正确,①错误D. ①②③都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
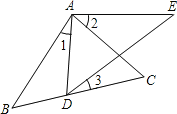
【题目】已知,如图△ABC与△ADE中,D在BC上,∠1=∠2=∠3
(1)求证:△ABC∽△ADE;
(2)若AB=4,AD=2,AC=3,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com