
【题目】一次函数![]() 的图象记作
的图象记作![]() ,一次函数
,一次函数![]() 的图象记作
的图象记作![]() ,对于这两个图象,有以下几种说法:
,对于这两个图象,有以下几种说法:
①当![]() 与
与![]() 有公共点时,
有公共点时,![]() 随
随![]() 增大而减小;
增大而减小;
②当![]() 与
与![]() 没有公共点时,
没有公共点时,![]() 随
随![]() 增大而增大;
增大而增大;
③当![]() 时,
时,![]() 与
与![]() 平行,且平行线之间的距离为
平行,且平行线之间的距离为![]() .
.
下列选项中,描述准确的是( )
A. ①②正确,③错误B. ①③正确,②错误
C. ②③正确,①错误D. ①②③都正确
【答案】D
【解析】
画图,找出G2的临界点,以及G1的临界直线,分析出G1过定点,根据k的正负与函数增减变化的关系,结合函数图象逐个选项分析即可解答.
解:
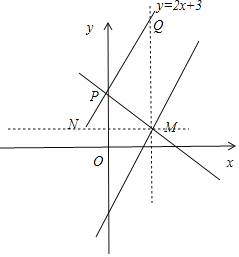
一次函数y2=2x+3(-1<x<2)的函数值随x的增大而增大,如图所示,N(-1,2),Q(2,7)为G2的两个临界点,
易知一次函数y1=kx+1-2k(k≠0)的图象过定点M(2,1),
直线MN与直线MQ为G1与G2有公共点的两条临界直线,从而当G1与G2有公共点时,y1随x增大而减小,故①正确;
当G1与G2没有公共点时,分三种情况:
一是直线MN,但此时k=0,不符合要求;
二是直线MQ,但此时k不存在,与一次函数定义不符,故MQ不符合题意;
三是当k>0时,此时y1随x增大而增大,符合题意,故②正确;
当k=2时,G1与G2平行正确,过点M作MP⊥NQ,则MN=3,由y2=2x+3,且MN∥x轴,可知,tan∠PNM=2,
∴PM=2PN,
由勾股定理得:PN2+PM2=MN2,
∴(2PN)2+(PN)2=9,
∴PN=![]() ,
,
∴PM=![]() ,故③正确.
,故③正确.
故选:D.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P在直线AB上方,且满足S△PABS:矩形ABCD=1:3,则使△PAB为直角三角形的点P有( )个
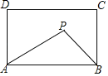
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 与点
与点![]() 关于原点对称,一次函数
关于原点对称,一次函数![]() 的图象经过点
的图象经过点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() .
.
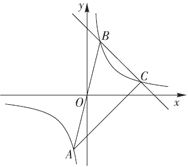
(1)求反比例函数与一次函数的表达式;
(2)求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某处有一座信号塔AB,山坡BC的坡度为1:![]() ,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
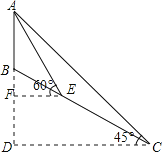
(1)求出山坡BC的坡角∠BCD的大小;
(2)求塔顶A到CD的铅直高度AD.(结果保留整数:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
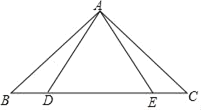
【题目】如图,在△ABC中,∠B=∠C=40°,点D、点E分别从点B、点C同时出发,在线段BC上作等速运动,到达C点、B点后运动停止.
(1)求证:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度数;
拓展:若△ABD的外心在其内部时,求∠BDA的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() 图象上一点,过点A作x轴的平行线交反比例函数y=﹣
图象上一点,过点A作x轴的平行线交反比例函数y=﹣![]() 的图象于点B,点C在x轴上,且S△ABC=
的图象于点B,点C在x轴上,且S△ABC=![]() ,则k=( )
,则k=( )
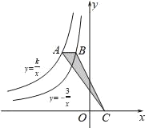
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)图象上,点B在反比例函数y=
(x>0)图象上,点B在反比例函数y=![]() (k>0,x>0)的图象上,AB∥x轴,BC∥y轴交x轴于点C,连结AC,交反比例函数y=
(k>0,x>0)的图象上,AB∥x轴,BC∥y轴交x轴于点C,连结AC,交反比例函数y=![]() (x>0)图象于点D,若D为AC的中点,则k的值是( )
(x>0)图象于点D,若D为AC的中点,则k的值是( )

A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com